Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 118
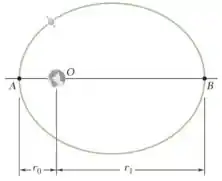
Um satélite descreve uma órbita elíptica em torno de um planeta. Representando por r0 e r1 as distâncias correspondentes, respectivamente, ao perigeu e ao apogeu da órbita, mostre que a curvatura da órbita em cada um desses pontos pode ser expressa como
Passo 1
Bem-vindo a mais uma questão de resmat que nos pede mostre que a curvatura da órbita em cada um desses pontos pode ser expressa como demonstrado no enunciado, então partiu !
Usando Eq.(12.39) do livro temos:
e
mas
para isso
Adicionando,
Passo 2
Nos Pontos A e B, a direção radial é normal ao caminho.
mas
Resposta
Exercícios de Livros Relacionados
O movimento do pino P é restringido pela fenda curva da lemniscata em O B e pela fenda do braço O A . Se O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = 3r a d / s , determine a i
O movimento do pino P é restringido pela fenda curva da lemniscata em O B e pela fenda do braço O A . Se O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = 3 t 3 / 2r a d / s , onde
O motorista do carro mantém uma velocidade escalar constante de 40 m / s . Determine a velocidade angular da câmera acompanhando o carro quando θ = 15 ° .
A caixa desce deslizando pela rampa helicoidal com uma velocidade escalar constante de v = 2m / s . Determine a intensidade da sua aceleração. A rampa desce uma distância vertical de 1m para cada volt
O pino move-se na fenda curva definida pela lemniscata e pela fenda no braço. Em θ = 30 ° , a velocidade angular é θ ˙ = 2r a d / s , e a aceleração angular é θ ¨ = 1,5r a d / s 2 . Determine as inten