Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 95
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial perpendicular a OA e se move sob a ação de uma força central F ao longo de uma trajetória elíptica definida elaequação r = / (2 – cos ). Mostre que F é inversamente proporcional ao quadrado da istância r da partícula ao centro de força O.
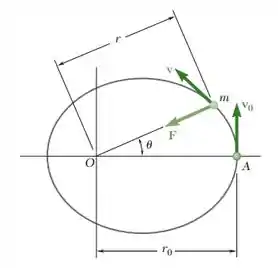
Passo 1
E ai gurizada tudo belezinha???
(a)
Resolução de F:
Uma vez que m, h e são contantes, F é proporcional a , ou inversamente proporcional a r².
Resposta
Uma vez que m, h e são constantes, F é proporcional a , ou inversamente proporcional a r².
Exercícios de Livros Relacionados
A barra O A gira no sentido anti-horário com uma velocidade angular constante de θ ˙ = 6r a d / s . Através de meios mecânicos, o anel B move-se ao longo da barra com uma velocidade escalar de r ˙ = 4
Por um curto período de tempo, um avião a jato move-se ao longo de uma trajetória de uma lemniscata, r 2 = 2500 cos 2 θk m 2 . No instante que θ = 30 ° , o equipamento rastreador de radar está giran
Um barco move-se ao longo de uma trajetória definida por r 2 = 0,9 10 3 cos 2 θm 2 , onde θ é dado em radianos. Se θ = 0,4 t 2r a d , onde t é dado em segundos, determine as componentes radiais e tr
A barra O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = ( 2 t 2 )r a d / s . Através de meios mecânicos, o anel B move-se ao longo da barra com uma velocidade escalar de r ˙ = 4 t
Uma partícula move-se ao longo de uma espiral de Arquimedes r = 8 θ m , onde θ é dado em radianos. Se θ ˙ = 4r a d / s (constante), determine as componentes radiais e transversais da velocidade e acel