Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 9

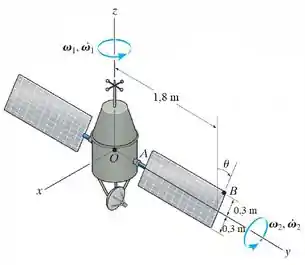
No instante quando θ = 90 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 15   r a d / s e aceleração angular ω ˙ 1 = 3   r a d / s 2 . Simultaneamente, os painéis solares giram com uma velocidade angular ω 2 = 6   r a d / s   e aceleração angular ω ˙ 2 = 1,5   r a d / s 2 . Determine a velocidade e a aceleração do ponto B no painel solar nesse instante.

Passo 1

O DCL abaixo mostra as velocidades e acelerações presentes no problema.

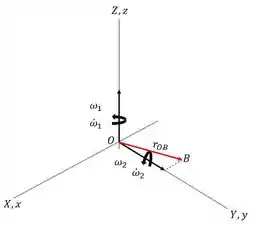
O painel solar rotaciona em torno do ponto fixo O . Uma vez que, no instante θ = 90 ° , o sistema fixo X Y Z coincide com o sistema relacionado x y z , então, a velocidade angular do painel pode ser obtida por

ω = ω 1 + ω 2 = 6 j + 15 k r a d / s

Passo 2

De modo semelhante, a aceleração angular é calculada por

α = ω ˙ = ω ˙ 1 + ω ˙ 2

Definindo o sistema de cordenadas x y z como referência para ter uma velocidade angular ω 1 , então, a velocidade angular ω 2 será constate em relação a x y z e sempre direcionada ao eixo y . Logo,

ω ˙ 2 = ω ˙ 2 x y z + ω 1 × ω 2 = 1,5 j + 15 k × 6 j = - 90 i + 1,5 j   r a d / s 2

ω ˙ 1 = ω ˙ 1 x y z + ω 1 × ω 1 = 3 k + ( 15 k × 15 k ) = 3 k   r a d / s 2

Portanto,

α = 3 k + - 90 i + 1,5 j = - 90 i + 1,5 + 3 k r a d / s 2

Passo 3

Como r O B = - 0,3 i + 1,8 j m , a velocidade no ponto B será

v B = ω × r O B = 6 j + 15 k × - 0,3 i + 1,8 j = - 27 i - 4,5 j + 1,8 k   m / s

E a aceleração no ponto B é igual a

a B = α × r O B + ω × ( ω × r O B )

a B = - 90 i + 1,5 + 3 k × - 0,3 i + 1,8 j + 6 j + 15 k × [ 6 j + 15 k × ( - 0,3 i + 1,8 j ) ]

a B = 72,9 i - 405,9 j + 0,45 k   m / s 2

Resposta

A velocidade e a aceleração no ponto B , no instante em que θ = 90 ° , são iguais a - 27 i - 4,5 j + 1,8 k   m / s   e 72,9 i - 405,9 j + 0,45 k   m / s 2 , respectivamente.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra A B está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A tem uma velocidade v A = 1,5 im / s e uma aceleração a A = 0,2 im / s 2 no instante mostrado, determine a acel
Se a manivela B C está girando com uma velocidade angular ω B C = 6r a d / s e uma aceleração angular ω ˙ B C = 1,5r a d / s 2 , determine a aceleração do anel A nesse instante. Suponha que a velocida
No instante mostrado, a cabine da escavadeira gira em torno do eixo z com uma velocidade angular constante ω z = 0,3r a d / s . No mesmo instante θ = 60 ° , e a lança O B C tem uma velocidade angular
No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an
O disco A gira a uma velocidade angular constante de 10r a d / s . Se a barra B C está ligada ao disco e ao anel por juntas esféricas, determine a velocidade do anel B no instante mostrado. Além disso