Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 43
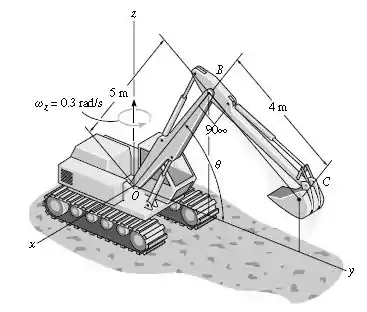
No instante mostrado, a cabine da escavadeira gira em torno do eixo com uma velocidade angular constante . No mesmo instante , e a lança tem uma velocidade angular , que está aumnetando a , ambas medidas em relação à cabine. Determine a velocidade e a aceleração do ponto na pá nesse instante.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos às analises:
Temos que:
Portanto:
Temos também que:
Resposta
Exercícios de Livros Relacionados
A placa triangular A B C está apoiada em A por uma junta esférica e em C pelo plano x - z . O lado A B encontra-se no plano x - y . No instante θ = 60 ° , θ ˙ = 2r a d / s , θ ¨ = 3r a d / s 2 e o pon
Resolva o exemplo 20.5 tal que os eixos x , y , z se desloquem com uma translação curvilínea, Ω = 0 no caso em que o anel parece ter uma velocidade angular Ω x y z = ω 1 + ω 2 e um movimento radial.
No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an
Resolva o problema 20.37 se a conexão em B consistir de um pino, como mostrado na figura, em vez de uma junta esférica. Dica: a restrição permite a rotação da barra tanto em torno da barra D E (direçã
O pequeno cilindro A está deslizando sobre a barra curva com velocidade u em relação à barra como mostrado. Simultaneamente, a barra está girando com velocidade angular ω em torno do ponto fixo B. Con