Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 222
No instante mostrado, os carros A e B movem-se a velocidade escalares de km/ h e km/h, respectivamente. Se A está aumentando a sua velocidade escalar na razão de km/h2 enquanto a sua velocidade escalar de B está reduzindo na razão de km/h2, determine a velocidade e aceleração de B em relação a A.
Passo 1
Os carros A e B se movimentando podem ser tratados como partículas para esse caso. Então, para se determinar a velocidade e aceleração de B em relação a A é necessário aplicar as equações que relacionam as velocidades e acelerações absolutas e relativas das partículas.
Passo 2
Como as equações de movimento relativo entre duas partículas são vetoriais é necessário determinar as componentes de cada vetor. Pela representação da figura acima, conclui-se que tem a seguite direção.
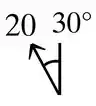
Então,
E o vetor tem componete somento na direção horizontal x, dado pela equação a seguir
Para as componentes de aceleração de A e B. o carro B está em trajetória curva logo, possui uma aceleração normal e tangencial. O modulo da aceleração normal de B pode ser determinado por
Sabendo que a aceleração normal está no sentido do centro da curva e aceleração tangencial tem modulo de km/h2 e está nadireçao da velocidade de B. o vetor pode ser descrito na direção x e y sendo,
Como carro A possuir trajetória retilínea, o vetor aceleração só tem componete na direção x.
Passo 3
Após todas as componentes de velocidade e aceleração determinadas é possível resolver o problema utilizando as equações velocidades e acelerações absolutas e relativas das partículas A e B.
Para a velocidade
km/h
E a direção pode ser calulada por
Para a aceleração,
Km/h2
E a direção pode ser calulada por,
Resposta
A velocidade de B em relação a A , e tem direção e seu modulo
A aceleração de B em relação a A , e tem direção e seu modulo Km/h2