Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 199
O navio está se dirigindo para o oeste a uma velocidade de nós, e o navio está se dirigindo para o sudeste. A direção relativa de com relação a é de e é invariável. Se a distância entre e é de milhas marítimas às horas, quando a colisão ocorreria se nenhum navio alterasse o curso?
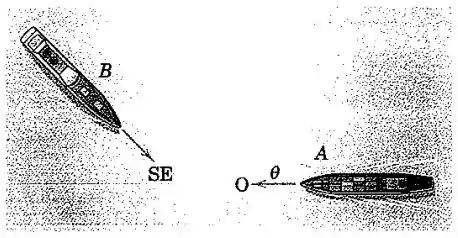
Passo 1
Vetorialmente, podemos escrever as velocidades de , e a velocidade relativa assim:
onde todas as velocidades são dadas em nós (ou milhas marítimas por hora).
Lembre-se que a relação entre as velocidades deve ser:
Olhando cada componente separadamente, isso resulta em duas equações:
Passo 2
As duas equações que acabamos de obter formam um sistema de duas equações e duas incógnitas, que ao resolvermos, encontramos:
Tendo conhecimento da velocidade relativa, podemos escrever a seguinte equação:
onde é a distância relativa em milhas entre os navios depois de horas contadas a partir de . Além disso, representa a distância relativa inicial, e a velocidade foi adotada como negativa porque os navios estão se aproximando.
Então, os navios se chocam quando , vamos substituir isso na equação:
Ou seja, a colisão ocorreria às .