Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 243
O carro tanspõe uma curva de de raio a uma velocidade constante de . Quando passa na posição mostrada, o carro está a do cruzamento e está acelerando para o sul rumo ao cruzamento na taxa . Determine a aceleração que parece ter quando observado por um ocupante de nesse instante.
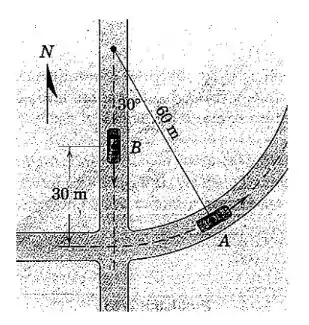
Passo 1
O segredo aqui é não confiar demais na sua intuição, porque às vezes os resultados são bem inesperados. Dê uma olhada na fórmula para a aceleração relativa:
Onde é a aceleraçao de em relação a . Vamos começar identificando os vetores das acelerações.
Como o carro tem velocidade constante, a única aceleração atuando sobre ele é a centrípeta:
E a aceleração do carro já foi dada no enunciado:
Vamos desenhar os vetores para fazer a soma!
Passo 2
Primeiro vamos colocar os vetores na figura (fora de escala):
E agora vamos organizar os vetores de forma que a soma fique mais simples de enxergar:
Lembrando de inverter o vetor já que temos aquele sinal negativo.
Agora é só usar um pouco de geometria plana para calcular aquele vetor preto. O ângulo de é o que foi dado na questão, e a gente pode deduduzir o ângulo fazendo o seguinte:
Agora é só aplicar a lei dos cossenos para calcular o módulo vetor preto :
Passo 3
Beleza, já temos o módulo da aceleração relativa, mas cuidado! A questão pediu a “aceleração”, ou seja, temos que indicar módulo, direção e sentido.
Para especificar aquelas duas últimas, seria suficiente dizer, por exemplo, o ângulo que o vetor aceleração forma com a direção norte (conforme indicado na figura do enunciado).
Vamos usar essa figura para calcular esse ângulo:
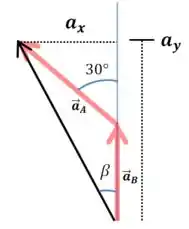
Onde e são as componentes do vetor :
Agora o ângulo é:
Pronto, esse é o ângulo que o vetor faz com o sentido norte.
Resposta
A aceleração observada por um ocupante de é de a noroeste.