Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 231

No instante t = 0 uma pequena bola é arremessada a partir do ponto A com uma velocidade de 60   m / s no ângulo de 60 ° . Despreze a resistência atmosférica e determine os dois instantes de tempo t 1 e t 2 quando a velocidade da bola faz um ângulo de 45 ° com o eixo horizontal x .

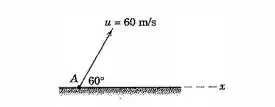
Passo 1

A velocidade vai fazer um ângulo de 45 ° com o eixo horizontal em duas ocasiões diferentes: uma vez na subida e uma vez na descida.

Qual é a principal propriedade desse ângulo de 45 ° ? A tangente dele é igual a 1 !

tan ⁡ 45 ° = 1

E o que é a tangente do ângulo do vetor velocidade? É a razão entre os módulos das componentes vertical e horizontal:

tan ⁡ θ = v y v x

Ou seja, estamos procurando os pontos em que:

v y = v x         ⇒         y ˙ = x ˙

Passo 2

Beleza, vamos escrever expressões para cada uma dessas velocidades.

A única aceleração envolvida nesse caso é a gravidade, que só afeta a componente vertical. Então:

x = x 0 + ( v o cos ⁡ 60 ° ) t

y = y o + v 0 sen ⁡ 60 ° t + a t 2 2

Considerando x 0 , y 0 = ( 0,0 ) e derivando as duas expresões:

x ˙ = v o cos ⁡ 60 °

y ˙ = v 0 sen ⁡ 60 ° + a t

Substituindo na nossa igualdade do passo 1 :

v o cos ⁡ 60 ° = v 0 sen ⁡ 60 ° + a t

Como adotamos o zero como estando no solo, teremos a = - g :

v o cos ⁡ 60 ° = v 0 sen ⁡ 60 ° - g t

Passo 3

Vamos substituir os valores numéricos:

v o cos ⁡ θ = v 0 sen ⁡ θ - g t

30 = | 51,96 - 9,81 t |

E as duas soluções vão ser as seguintes:

51,96 - 9,81 t 1 = 30

9,81 t 2 - 51,96 = 30

Resolvendo essas equações encontramos:

t 1 = 2,24   s

t 2 = 8,35   s

Resolvido!

Resposta

Os dois instantes de tempo são t 1 = 2,24   s e t 2 = 8,35   s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma parte de uma loja de departamento, um trem de ferromodelismo D corre em uma leve inclinação vista entre duas escadas rolantes de subida e descida. Quando o trem e os compradores passam pelo pon
Quando um pequeno barco viaja para o norte a 5 km/h, uma bandeira montada na sua popa forma um ânguloθ = 50° com a linha central do barco, como mostrado na figura. Pouco depois, quando o barco está vi
Um motorista que dirige ao longo de um trecho de reta de uma rodovia diminui a velocidade de seu automóvel para uma taxa constante antes de sair da rodovia em direção a uma rampa de saída circular com
A partir de uma fotografia do dono de uma casa utilizando um removedor de neve determina-se que o raio de curvatura da trajetória da neve foi de 8,5 m a partir do momento em que ela deixa o cano de de
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0. (a) Mostre que o raio de curvatura da trajetória do projétil alcança seu valor mínimo no ponto mais alto B da trajetória. (b)