Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 234

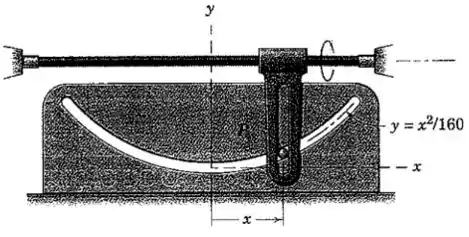
Para um determinado intervalo de movimento, o pino P é forçado a se deslocar na ranhura fixa parabólica pela guia vertical ranhurada, que se desloca na direção x na taxa constante de 20   m m / s . Todas as medidas estão em milímetros e segundos. Calcule os módulos da velocidade v e da aceleração a do pino P quando x = 60   m m .

Passo 1

A primeira informação que o enunciado dá é uma relação entre as coordenadas do pino:

y = x 2 160

Além disso temos a velocidade do pino na direção x :

x ˙ = 20   m m / s

Nosso objetivo é calcular a velocidade e a aceleração do pino. Isso quer dizer que precisamos achar os valores de x ˙ , y ˙ , x ¨ e y ¨ .

Passo 2

Já temos x ˙ , então vamos derivar a primeira relação para encontrar y ˙ :

y = x 2 160

d d t y = d d t x 2 160

y ˙ = 1 160 d x 2 d t = 1 160 d x 2 d x   d x d t

y ˙ = 1 80 x x ˙

E então a fórmula da velocidade é:

v = ( x ˙ ) 2 + 1 80 x x ˙ 2

No caso em que x ˙ = 20   m m / s e x = 60   m m temos:

v = 25   m m / s

Passo 3

Agora fazemos fazer algo bastante parecido para a aceleração. Começando pela coordenada y :

y ¨ = d d t 1 80 x x ˙

y ¨ = 1 80 ( x x ¨ + x ˙ x ˙ )

Mas como x ˙ é constante, então x ¨ = 0 .

y ¨ = 1 80 x ˙ 2

Por isso a aceleração é simplesmente:

a = y ¨ = 1 80 20 2 = 5   m m / s 2

Resposta

A velocidade tem módulo v = 25   m m / s e a aceleração é a = 5   m m / s 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
Um barco está se movendo ao longo da trajetória circular com uma velocidade escalar de v = 0,0625 t 2m / s , onde t é dado em segundos. Determine a intensidade da sua aceleração quando t = 10s .
Quando x = 3m , o caixote tem uma velocidade escalar de 6m / s que está aumentando a 1,8m / s 2 . Determine a direção da velocidade do caixote e a intensidade da aceleração do caixote nesse instante.
Se o carro desacelera uniformemente ao longo da estrada curva de 25m / s em A para 15m / s em C, determine a aceleração do carro em B.