Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 69

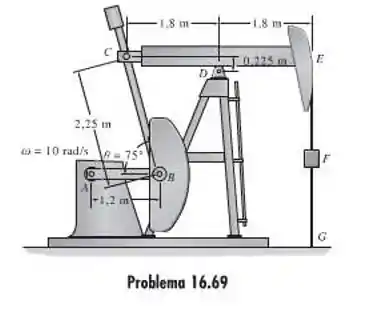
69. A unidade de bombeamento consiste da manivela AB, barra de ligação BC, balancim CDE e tirante F. Se a manivela está girando com uma velocidade angular ω=10 rad/s, determine a velocidade angular do balancim e a velocidade do tirante EFG no instante mostrado.

Passo 1

Fala galerinha, tudo certo? Pra resolver esse problema vamos separar a nossa estrutura em várias partes e fazer o DCL de cada uma delas, assim a gente pode encontrar relações entre as velocidades angulares e enfim encontrar a velocidade angular do balancim CDE e do tirante EFG.

Vamos começar com a barra AB.

A velocidade de B é expressa como

v B = ω × r B

Nesse sentido, temos

v B = - 10 k × { 1,2 i }

v B = { - 12 j }

Passo 2

Agora vamos olhar o balancim CDE, e tirar algumas relações importantes.

A velocidade de C é expressa como

v C = ω C D E × r D C

Substituindo as distâncias.

v C = { ω C D E k } × { - 1,8 i + 0 , 225 j }

v C = { - 0 , 225 × ω C D E i - 1,8 ω C D E j }

A velocidade de E é expressa como

v E = ω C D E × r D E

E aí substituindo.

v E = ω C D E k × 1,8 i }

v E = { 1 , 8 ω C D E j }

Passo 3

Por fim vamos analisar a barra CB.

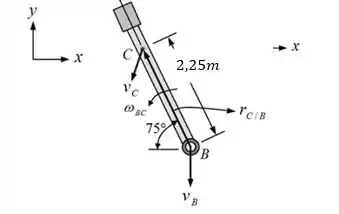
A partir da equação da velocidade, temos

v C = v B + ω B C × r C / B

O vetor de posição direcionado de B para C é expresso como

r C / B = - 2,25 cos ⁡ 75 ° i + 2,25 sin ⁡ 75 ° j   m

r C / B = - 0,582 i + 2,17   j m

Ao substituir os valores dos parâmetros em na equação da velocidade a gente encontra:

- 0,225 × ω C D E i - 1,8 ω C D E j = - 12 j + { ω B C k } × - 0,582 i + 2,17   j m

- 0,225 × ω C D E i - 1,8 ω C D E j = - 12 j + - 2,17   ω B C i - 0,582 ω B C j m

Passo 4

Ao equacionar os coeficientes i na equação encontrada no passo 3, obtemos

- 0,225 × ω C D E = - 2,17 ω B C

ω C D E = 2,17 0,225 ω B C = 9,64 ω B C

ω B C = ω C D E 9,64

Ao equacionar os coeficientes j, obtemos da equação:

- 0.582 ω B C - 12 = - 1.8 ω C D E

Rearrumando.

1,8 ω C D E = 12 + 0,582 ω B C

Substituindo ω B C = ω C D E 9,64

1,8 ω C D E - 0,582 ω C D E 9,64 = 12

1,74 ω C D E = 12

ω C D E = 12 1,74 = 6,89   r a d / s

A velocidade angular do balancim é  ω C D E = 6,89   r a d / s  

Ao substituir o valor encontrado anteriormente na equação da velocidade da barra E, temos

v E = 1,8 × 6,89 j m / s

v E = 12,4 j m / s

Resposta

ω C D E = 6,8 9   r a d / s

v E = 12 , 4 j m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.59. Uma cremalheira reta repousa sobre uma engrenagem de raio r e está presa ao bloco B como mostra a figura. Representando por D a velocidade angular horária da engrenagem D e por o ângulo formado
15.60. Uma cremalheira reta repousa sobre uma engrenagem de raio r 75 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade angular da engrenagem D é de 15 rpm no se
15.58. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.