Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 139
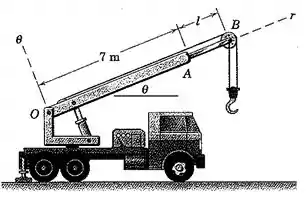
2/139) A haste gira em torno do ponto , enquanto a seção simultameamente prolonga-se de dentro da seção . Determine a velocidade e a aceleração do centro da polia para as seguintes condições : , , , , . As grandezas e são a primeira e a segunda derivadas , respectivamente , do comprimento da seção .
Passo 1
Bom galera , nós sabemos que a velocidade é dada por :
Antes, vamos fazer uma conversão no valor de , passando-o para radianos por segundo:
Isso é necessário pois a resposta final deve estar toda em
Substituindo os valores que conhecemos , obtemos que :
Passo 2
Da mesma forma , aceleração é dada por :
Sendo assim , temos que :
Resposta
De boa pessoal? Bora continuar então
Exercícios de Livros Relacionados
Mostre que o momento angular por unidade de massa h de um satélite que descreve uma órbita elíptica de semieixo maior a e excentricidade ε , em torno de um planeta de massa M, pode ser expresso como h
Um satélite descreve uma órbita elíptica em torno de um planeta. Representando por r0 e r1 as distâncias correspondentes, respectivamente, ao perigeu e ao apogeu da órbita, mostre que a curvatura da ó
Uma partícula de massa m descreve uma trajetória definida pela equação r = r 0 sen θ sob uma força central F voltada para o centro de força O. Mostre que F é inversamente proporcional àquinta potência
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v 0 perpendicular a OA e se move sob a ação de uma força central F ao longo de uma trajetória elíptica definida elaequação r =
Uma partícula de massa m descreve uma cardioide r = r 0 (1 cos θ /2) sob uma força central F voltada para o centro de força O. Usando a Eq. (12.37), mostre que F é inversamente proporcional ao quadrad