Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 195

No instante representado x = 50 mm e s ˙ = 1,6   m / s . Determine a velocidade correspondente do ponto B.

Passo 1

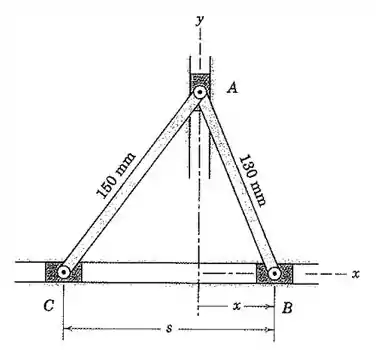
Bom pessoal, outro exercício que a geometria é importante para a resolução. Então, vamos fazer um esboço do sistema colocando as velocidades em destaque:

Beleza, agora vamos mostrar de onde saiu esses valores.

Por pitágoras, podemos calcular a mediana AP:

A P = 130 2 - 50 2 = 120

Com AP, podemos calcular CP:

C P = 15 0 2 - 12 0 2 = 90

Com isso, sabemos as relações dos angulos θ   e   β . Isto será importante para descobrir as relações entre os vetores velocidades.

Passo 2

Pelo enunciado, a velocidade relativa entre B e C vale 1,6 m/s:

s ˙ = 1,6 = v B / C = v B - v C

Pela equação da velocidade relativa, também temos as seguintes relações de vetores:

v B = v A + v B / A

v C = v A + v C / A

Se diminuirmos essas duas equações, achamos que:

v B - v C = v B / A - v C / A

Bom, nós podemos traçar agora o diagrama de vetores:

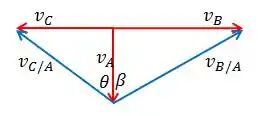
Como já sabemos as relações dos ângulos, podemos tirar algumas relações também das velocidades:

v A = v C t a n θ = v B t a n β

v C 90 120 = v B 50 120

Podemos montar o sistema de equações:

v B + v C = 1,6

v C = 5 9 v B

Resolvendo:

v B = 1,029

v C = 0,571

Resposta

v B = 1 , 029   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.59. Uma cremalheira reta repousa sobre uma engrenagem de raio r e está presa ao bloco B como mostra a figura. Representando por D a velocidade angular horária da engrenagem D e por o ângulo formado
15.60. Uma cremalheira reta repousa sobre uma engrenagem de raio r 75 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade angular da engrenagem D é de 15 rpm no se
15.58. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.