Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 198
A fita está sendo transferida do rolo A para o rolo B. Se o rolo B gira com uma velocidade angular constante determine uma expressão para a aceleração angular do rolo A em um instante qualquer quando os raios da fita A e de B são respectivamente. A espessura da fita é b. Despreze o movimento angular muito pequeno da fita entre os rolos.
Passo 1
Bom pessoal, vamos fazer um esboço do sistema de rolos da questão.
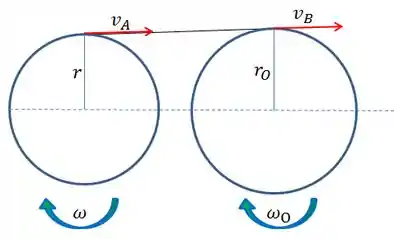
Sendo a velocidade da fita a mesma por toda sua extensão, temos que:
Derivando a igualdade acima em função do tempo, temos que:
Como o enunciado diz que o rolo B gira a velocidade constante, então :
O raio dos rolos cresce de acordo com a espessura b da fita. Relacionando estas variáveis, temos:
Onde n é o número de voltas da fita. Derivando a expressão em função do tempo:
Importante!!! O sinal de negativo é porque o rolo A está diminuindo a espessura.
Para o rolo B, teremos então que
Então, voltando para a expressão (1):