Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 194
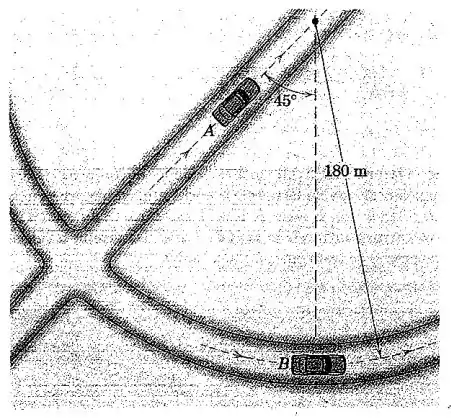
Para o instante representado, o carro tem uma aceleração na direção do seu movimento, e o carro tem uma velocidade de que está aumentando. Se a aceleração de como observada a partir de é nula para esse instante, determine a aceleração de e a taxa em que a velocidade de está variando.
Passo 1
A aceleração do carro , por ser na mesma direção da reta de sua trajetória, pode ser escrita assim:
sendo que pode ser pode ser positiva ou negativa, dependendo de o carro estar aumentando ou reduzindo sua velocidade.
Já o carro tem duas acelerações, a normal e a tangencial. A aceleração tangencial ocorre no sentido positivo do eixo , pois o carro está aumentando sua velocidade:
A aceleração normal de aponta para o centro do círculo, ou seja, para o sentido positivo do eixo , e então:
Como a aceleração de deve ser a soma das componentes tangencial e normal, temos:
Passo 2
Então, a aceleração relativa do carro em relação ao carro será:
Porém, o enunciado nos diz que essa aceleração relativa é nula no instante considerado. Logo, podemos igualar cada componente a zero. Começamos com a componente de :
Agora a componente de :
Assim concluímos que o carro tem uma aceleração de no sentido de seu movimento e o carro varia sua velocidade numa taxa de .