Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 161
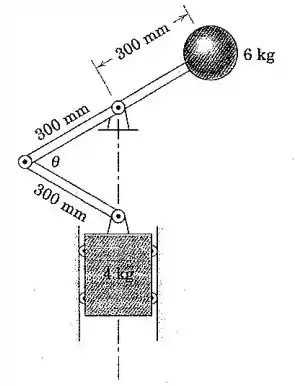
Quando o mecanismo é liberado a partir do repouso na posição em que , o carro de cai e a esfera de sobe. Determine a velocidade da esfera quando . Despreze a massa das conexões e trate a esfera como uma partícula.
Passo 1
A energia mecânica inicial do sistema é a soma das energias mecânicas dos corpos e , de e de , respectivamente. Ela se expressa assim:
Pela geometria da figura, e considerando a altura do suporte fixo como a altura zero, temos:
pois forma-se ali um triângulo equilátero (dois lados já eram iguais e ).
Para calcular , repare que o ângulo com a horizontal vai ser , metade de :
Calculamos então a energia inicial:
Passo 2
Na posição final, quando , o corpo tem apenas velocidade horizontal, e portanto, o corpo tem velocidade nula. Então, a energia final é pode ser expressa desse modo:
Como os dois corpos ficam completamente na vertical, as alturas passam a ser:
Então será:
Passo 3
Pela conservação da energia mecânica total do sistema, temos: