Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 29

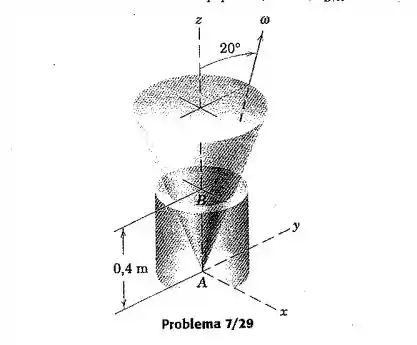
O cilindro maciço possui um cone do corpo com um semi-ângulo do vértice de 20º. Em um determinado instante a velocidade angular ω tem um módulo de 30 rad/s e está situada no plano y - z . Determine a taxa p na qual o cilindro está girando em torno do seu eixo z e escreva a expressão vetorial para a velocidade de B em relação a A .

Passo 1

Para o problema em questão, temos que o cilindro estará girando com uma velocidade p , que queremos descobrir, e a mesma aponta na direção de z . Para resolvermos então, iremos usar as relações de ângulo e após isso usaremos a definição de velocidade relativa de um ponto de referência para encontrarmos a velocidade de B .

Passo 2

Como foi dito no passo 1, temos que a velocidade angular total do sistema, ω , está situada no plano y - z , porém a velocidade do cilindro apenas estará situada apenas uma direção, z , que será dada pela relação

p = ω ⋅ cos ⁡ 20 º ⋅ k ^ = ( 30   r a d / s ) ⋅ ( 0.9397 ) ⋅ k ^ = 28.2   r a d / s

Passo 3

Para a velocidade de um ponto em relação a outro, temos que é dada pela equação

v B A = ω × r B A

Onde ω = ω y ⋅ s e n 20 º ⋅ j ^ + ω z ⋅ cos ⁡ 20 º ⋅ k ^ e r B A = 0.4 ⋅ k ^ . Calculando, teremos que:

v B A = ω × r B A = ω y ⋅ r B A ⋅ i ^ = 4.10 ⋅ i ^   m / s  

Resposta

p =   28.2   r a d / s

v B A = 4.10 ⋅ i ^   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ventilador de 4 pás gira em torno do eixo fixo OB com uma velocidade angular constante de N = 1200 rpm. Escreva as expressões vetoriais para a velocidade v e a aceleração a da extremidade A da pá do
O disco circular está girando em torno do eixo OC com velocidade angular constante ω =20r a d / s . Em um determinado instante, o ponto A sobre a borda passa por um ponto cujas coordenadas x-y-z são 4
A barra é articulada em torno do eixo O-O do garfo, eu está preso à extremidade do eixo vertical. O eixo gira com uma velocidade angular constante ω 0 como mostrado. Se θ está diminuindo na taxa const
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
A haste vertical e o seu garfo vinculado giram em torno do eixo z na taxa constante Ω = 4r a d / s . Simultaneamente, a haste B gira em torno de seu eixo AO na taxa constante de w0 = 3 rad/s e o ângul