Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 101
Um pequeno cursor de massa recebe uma velocidade inicial de módulo sobre a guia horizontal circular fabricada a partir de uma haste delgada. Se o coeficiente de atrito dinâmico é , determine a distância percorrida antes de o cursor atingir o repouso. (Sugestão: Observe que a força de atrito depende da força normal resultante.)
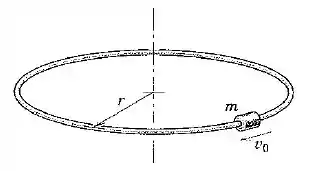
Passo 1
A força normal cumpre dois papéis nesse movimento: existe uma componente que compensa o peso do cursos (apontando para cima), e outra que mantém a trajetória circular (apontando para o centro do círculo):
Então a força normal total é:
E então a força de atrito é:
Que age na direção tangencial, porque é sempre contrário ao movimento do corpo.
Passo 2
Essa força de atrito produz uma desaceleração:
E como podemos relacionar isso com a distância percorrida pelo cursor?
E então:
Vamos integrar:
Passo 3
Agora precisamos resolver essa integral.
Vamos usar uma substituição:
E agora podemos consultar a tabela de integrais no final do livro e aplicar essa fórmula:
E então:
E agora podemos substituir de volta :
E essa é a distância que o cursor percorre até parar.
Resposta
A distância percorrida até o repouso é .