Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 82

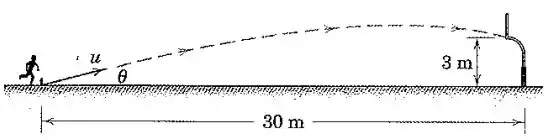
Um jogador de futebol americano tenta um chute de 30   m passando a bola sobre a barra horizontal e entre os postes da trave. Se ele é capaz de transmitir uma velocidade u de 30   m / s à bola, calcule o ângulo mínimo θ para o qual a bola irá transpor a barra horizontal do gol. (Sugestão: Faça m = t g   θ .)

Passo 1

Galera, para que a bola transponha a barra horizontal do gol, precisamos que, quando x = 30   m , tenhamos y ≥ 3   m , considerando o ponto do chute no chão como a origem do sistema de coordenadas. Então, se tivermos a equação da trajetória parabólica que a bola faz, ou seja, se encontrarmos uma equação que nos dê y em função de x , poderemos encontrar o ângulo mínimo θ .

Pra obtermos isso, começamos equacionando o movimento horizontal:

x = x 0 + v x t = u cos ⁡ θ   t

t = x u cos ⁡ θ

Para o movimento vertical, teremos:

y = y 0 + v 0 y t - 1 2 g t 2 = u   s e n   θ   t - 1 2 g t 2

Substituiremos a expressão de t encontrada:

y = u   s e n   θ x u cos ⁡ θ - 1 2 g x 2 u 2 cos 2 ⁡ θ

y = t g   θ   x - g 2 u 2 cos 2 ⁡ θ x 2

Aí temos a nossa equação da trajetória!

Passo 2

Para que tenhamos θ como o ângulo mínimo, vamos substituir, na equação da trajetória, x = 30   m e y = 3   m , beleza? E também u = 30   m / s segundo o enunciado e g = 9,8   m / s :

3 = 30   t g   θ - 9,8 2 30 2 cos 2 ⁡ θ 30 2

3 = 30   t g   θ - 4,9 sec 2 ⁡ θ

Lembre-se daquela relação trigonométrica 1 + t g 2 θ = sec 2 ⁡ θ :

3 = 30   t g   θ - 4,9 - 4,9   t g 2 θ

4,9   t g 2 θ - 30   t g   θ + 7,9 = 0

t g   θ = 0,276                     o u                     t g   θ = 5,847

Em ângulos 0 ° < θ < 90 ° , quanto maior for a tangente, maior será o ângulo. Isso significa que, entre as duas soluções possíveis, o ângulo mínimo será:

θ = t g - 1 0,276 = 15,4 °

Resposta

θ = 15,4 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um garoto em A tenta jogar uma bola sobre o telhado de um celeiro de tal maneira que ela é lançada em um ângulo de θ A = 40 ° . Determine a velocidade mínima v A que ele deve jogar a bola de maneira q
Se a posição de uma partícula é definida por s = 2 sen ⁡ π 5 t + 4 m , onde t é dado em segundos, construa os gráficos s - t , v - t e a - t para 0 ≤ t ≤ 10 s.
Um míssil de dois estágios é lançado verticalmente a partir do repouso com a aceleração mostrada. Em 15 s, o primeiro estágio A esgota-se e o segundo estágio B dá partida. Elabore os gráficos v - t e
As cavilhas A e B estão restritas a moverem-se nas fendas elípticas devido ao movimento da fenda da barra. Se a fenda da barra se desloca com uma velocidade escalar constante de 10 m/s, determine a in
A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = ( 2 θ ) m. No instante θ = π / 4 rad, a velocidade angular e a aceleração angular do anel garfo são θ ˙