Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 37

Calcule a velocidade angular ω da barra esbelta A B como uma função da distância x e da velocidade angular constante ω 0 do tambor.

Passo 1

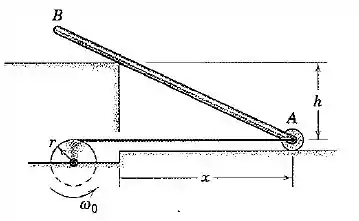
Conforme o tambor gira e enrola o fio, a barra é puxada pela roda A . A velocidade com que o fio se enrola no tambor é:

v A = ω 0 r

Que é justamente a velocidade com que A se desloca para a esquerda (por isso o sinal negativo):

x ˙ = - ω 0 r

Nosso objetivo é encontrar a velocidade angular da barra, então precisamos escrever mais algumas relações geométricas.

Passo 2

Vamos chamar de θ o ângulo que a barra forma com o cabo. Nesse caso temos:

h = x tan ⁡ θ

E agora se derivarmos em relação ao tempo (considerando que h é uma constante):

0 = x ˙ tan ⁡ θ + x θ ˙ sec 2 ⁡ θ

E θ ˙ = ω é a velocidade angular que queremos encontrar:

θ ˙ = - x ˙ tan ⁡ θ x sec 2 ⁡ θ = - x ˙ x sen ⁡ θ cos ⁡ θ

Agora vamos retomar o desenho para escrevermos algumas relações para o seno e o cosseno do ângulo θ :

sen ⁡ θ = h h 2 + x 2

cos ⁡ θ = x h 2 + x 2

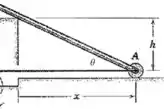
E então:

θ ˙ = - x ˙ x sen ⁡ θ cos ⁡ θ

θ ˙ = ω 0 r x h h 2 + x 2 x h 2 + x 2

θ ˙ = r   h   ω 0 x 2 + h 2

Resposta

A velocidade angular da barra é θ ˙ = r   h   ω 0 x 2 + h 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa retangular uniforme tem uma massa de 5 k g e é mantida na posição por três cordas como mostrado na figura. Sabendo que θ = 30 ° , determine, imediatamente depois da corda CF ter sido cortada
A empilhadeira mostrada na figura tem massa de 1.125 k g e é usada para elevar um caixote de massa m = 1,250 k g . A empilhadeira está se movendo para a esquerda com velocidade de 3 m / s quando os fr
Uma estrutura soldada triangular ABC é guiada por dois pinos que deslizam livremente em rasgos curvos paralelos de raio 150 mm cortados em uma placa vertical. A estrutura soldada tem uma massa de 8 kg
Três barras, cada uma de massa de 4 kg, são soldadas juntas e unidas por pinos a duas hastes de conexão BE e CF. Desprezando o peso das hastes de conexão, determine a força em cada haste de conexão im
Um prato uniforme circular de massa de 3 kg é unido a duas hastes de conexão AC e BD de mesmo comprimento. Sabendo que o prato é solto a partir do repouso na posição mostrada na figura, determine (a)