Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 9
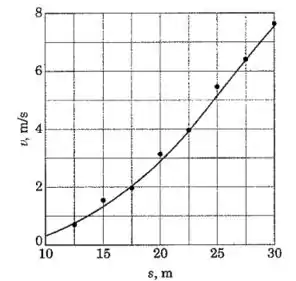
Dados experimentais para o movimento de uma partícula ao longo de uma linha reta forneceram medidas dos valores da velocidade para várias coordenadas de posição . Uma curva suave é desenhada passando pelos pontos como se pode ver no gráfico. Determine a aceleração da partícula quando
Passo 1
Temos um gráfico da velocidade em função da posição de uma partícula, e queremos calcular a aceleração em certo ponto. Vamos lembrar de algumas relações envolvendo essas grandezas:
Isolando nas duas equações, podemos chegar na seguinte igualdade:
Ou então:
Passo 2
Beleza, agora vamos pensar no que essa fórmula diz:
A derivada é a inclinação da reta tangente ao gráfico da função , que é justamente o gráfico que temos no enunciado.
Vamos pegar dois pontos próximos de e aproximar a curva por uma reta.
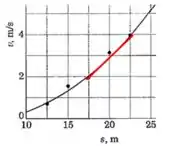
Pelo desenho dá pra ver que, quando estamos bem próximos do ponto em questão, a reta é uma excelente aproximação.
A derivada vai ser simplesmente a inclinação dessa reta:
Passo 3
Como estamos interessados no ponto onde podemos usar o gráfico para estimar que nesse momento temos .
E agora, retomando a nossa fórmula de antes, podemos fazer uma boa aproximaçaõ para a aceleração:
Pronto!
Resposta
A aceleração é aproximadamente nesse ponto.