Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 10
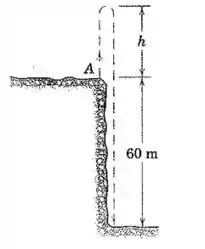
Uma bola é lançada verticalmente para cima com uma velocidade de na borda de um penhasco com . Calcule a altura para a qual a bola se eleva e o tempo total após a liberação para a bola alcançar o fundo do penhasco. Despreze a resistência do ar e considere a aceleração para baixo como .
Passo 1
Vamos começar pensando na trajetória entre o momento em que a bola é lançada e o momento que ela atinge a altura máxima .
Essa é uma trajetória bastante simples de calcular, porque a aceleração é constante para baixo e nós já temos a velocidade inicial:
Integrando em relação ao tempo:
Quando a bola atinge a altura máxima a velocidade necessariamente se anula, ou seja .
E substituindo os valores numéricos:
E esse é o tempo que a bola leva para atingir a altura máxima.
Passo 2
Agora, para encontrar a altura é só calcular quanto a partícula sobe nesse intervalo de tempo.
Integrando mais uma vez a nossa função lá de cima:
E substituindo , e .
E essa é a altura máxima que a bola atinge:
Passo 3
Agora falta calcular o tempo que a bola demora para atingir o solo a partir da altura máxima.
Vamos esquecer os referenciais que usamos até aqui, porque eles seriam inconvenientes. No topo da trajetória, a distância entre a bola e o solo é:
E o tempo que um objeto solto a partir do repouso demora para cair essa distância sob ação da gravidade é:
Somando com o tempo que calculamos anteriormente:
Pronto!
Resposta
A bola se eleva a do chão, e o tempo total da trajetória é aproximadamente .