Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 116
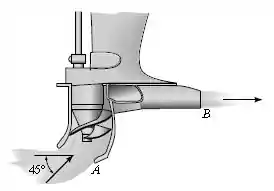
Uma lancha é propelida pelo motor a jato mostrado na figura. A água do mar é puxada pela bomba, a uma vazão de , através de uma entrada , de de diâmetro. Uma hélice acelera a vazão de água e a força para fora horizontalmente, através de uma saída de de diâmetro, . Determine as componentes horizontal e vertical do empuxo exercidas sobre a lancha. O peso específico da água do mar é .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Por definição, podemos relacionar a velocidade com a vazão:
Sabemos também que:
Bom galera, temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
A bola de 1,5k g , localizada em A , é liberada do repouso e move-se para baixo sobre a trajetória curva. Se a bola exerce uma força normal de 25N sobre a trajetória quando alcança o ponto B , determi
O projétil de massa 3k g é disparado de um canhão a uma velocidade na boca do canhão v O = 500m / s . Determine a quantidade de movimento angular do projétil em relação ao ponto O no instante que ele
Inicialmente o bloco de 5k g está girando a uma velocidade escalar constante de 2m / s , em relação à trajetória circular centrada em O , sobre o plano horizontal liso. Se uma força tangencial constan
A partícula A de 2k g tem a velocidade mostrada. Determine sua quantidade de movimento angular H O em relação ao ponto O .
A esfera de 2k g está presa em uma barra leve e rígida, que gira no plano horizontal centrada em O . Se o sistema está sujeito a um momento de binário M = 0,9 t 2 N ⋅ m , onde t está em segundos, dete