Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 95
A bola de , localizada em , é liberada do repouso e move-se para baixo sobre a trajetória curva. Se a bola exerce uma força normal de sobre a trajetória quando alcança o ponto , determine a quantidade de movimento angular da bola em relação ao centro de curvatura, ponto . Dica: despreze a dimensão da bola. O raio de curvatura no ponto deve ser determinado primeiro.
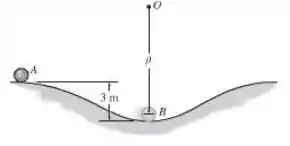
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos aplicar a conservação de energia entre o ponto e , para descobrir a velocidade no ponto :
Agora, a partir do somatório de forças na direção normal, vamos encontrar o raio de giração:
Portanto, a quantidade de movimento angular em é:
Resposta
Exercícios de Livros Relacionados
Uma viga engastada AB suporta um bloco que causa uma deflexão estática de 50 mm em B. Considerando que o suporte em A sofre um deslocamento vertical periódico δ = δ ms e nω ƒ t ƒ , onde, δ m = 12m m ,
Um cursor de 5 kg pode deslizar sobre uma barra horizontal sem atritoe está ligado a uma mola de constante k. Sobre ele atua uma força periódica de intensidade P = P ms e nω ƒ t ƒ , onde P m = 10N e ω
Um bloco A de 8 kg desliza em uma fenda vertical sem atrito e está ligado a um suporte móvel B por meio de uma mola de constante k = 120 N/m. Sabendo que a aceleração do suporte é a = a ms e nω ƒ t ,o
Um disco uniforme de 8 kg e raio de 200 mm é soldado a um eixo vertical com uma ponta engastada em B. O disco gira em um ângulo de 3° quando um binário estático de intensidade de 50N ∙ m lhe é aplicad
A barra AB é rigidamente presa à estrutura de um motor em funcionamento com velocidade constante. Quando um cursor de massa m é colocado sobre a mola, observa-se que ele tem amplitude de 15 mm. Quando