Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 54
Se o cilindro hidráulico BE exerce uma força vertical F = 1,5 kN sobre a plataforma, determine a força desenvolvida nos membros AB e CD no instante . A plataforma está em repouso quando . Despreze a massa dos membros e da plataforma. A caixa de 200 kg não desliza sobre a plataforma.
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
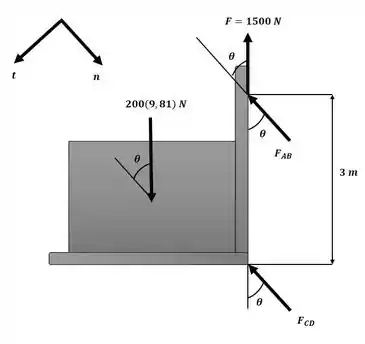
Separando a caixa e a plataforma, podemos decompor a aceleração angular em uma aceleração normal e outra tangencial, sendo:
Com isso, podemos aplicar um somatório de forças na direção tangencial ao braço AB, conforme ilustrado na figura a seguir, para descobrir uma relação entre e :
Passo 2
Utilizando o resultado obtido no passo 1, a velocidade angular deve ser obtida através de uma integração, uma vez que a aceleração não é constate.
Logo, quando:
Passo 3
Sendo assim, analisando o sistema com a inclinação de conforme ilustrado na figura a seguir:
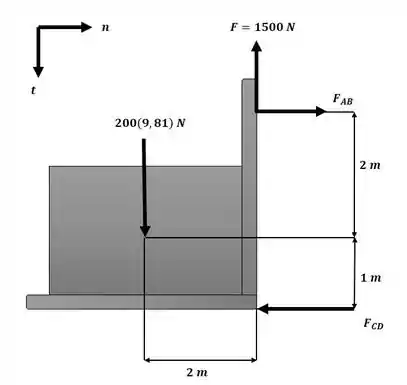
Podemos aplicar um somatório de forças na direção normal (equivalente a direção x com o sistema agora rotacionado) e um somatório de momentos em torno do centro de massa da caixa:
Isolando dessa última equação e substituindo na equação superior, temos:
E, substituindo esse valor na equação do somatório de momentos, obtemos :