Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 79
O motor V-8 de está apoiado em um suporte e girado de em relação a sua posição, de forma que seu centro de gravidade está na posição mostrada. Determine a reação vertical em cada roda do suporte. Despreze o peso do suporte.
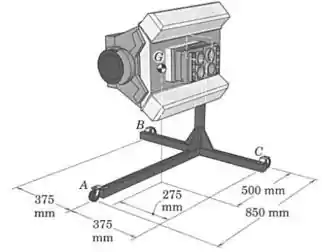
Passo 1
Vamos começar definindo os eixos e desenhando as forças que atuam no sistema:
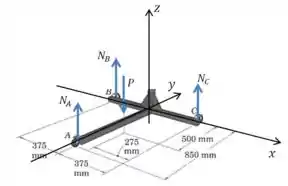
Ok, temos três variáveis desconhecidas, então precisamos montar três equaçãos de equilíbrio para poder resolver o problema.
Passo 2
Como todas as forças são paralelas ao eixo , não temos nenhum momento nessa direção, e essa não seria uma equação útil. Vamos considerar o momento em relação aos outros dois eixos.
As únicas forças que exercem momento em torno do eixo são e (já que e cruzam o eixo). favorece rotação no sentido horário, e no anti-horário:
Agora em torno do eixo : e favorecem o sentido anti-horário, o horário. A força cruza o eixo , e então não produz momento.
Ok, já temos duas equações, falta uma.
Passo 3
Vamos considerar o equilíbrio das forças:
Ok, agora temos um sistema de três variáveis e três equações:
Como a primeira equação dá:
Substituindo isso terceira:
E substituindo isso na segunda:
E agora é só substituir no resultado de antes:
Resposta
As forças são , e .