Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 77
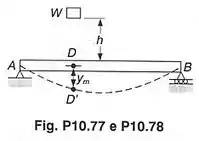
Um bloco de peso é abandonado de uma altura acima de uma viga horizontal , e choca-se com ela no ponto . Pede-se:
- Mostrar que a máxima deflexão no ponto pode ser expressa por
- para a barra e carregamento do Prob. 10.72, calcular o fator dinâmico.
onde representa a deflexão em provocada por uma carga estática aplicada nesse ponto, e onde a quantidade entre parênteses é chamada coeficiente de impacto ou fator dinâmico;
Passo 1
Fala, pessoal! Como estão os estudos? Bora fazer um exercício de carga produzida por choque?
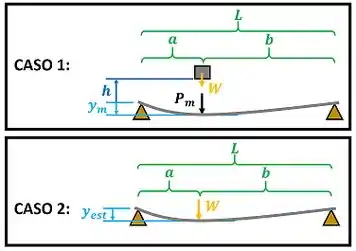
O enunciado quer primeiro que a gente compare a deformação sofrida por uma mesma viga em dois casos. No caso 1 a viga sofre o impacto de um bloco de peso que é largado a uma altura da viga. Esse impacto gera uma força na viga e gera uma deflexão no ponto da viga onde ocorre o impacto. Nesse caso, a energia potencial do bloco é absorvida pela viga.
No caso 2, uma força estática é aplicada no ponto da viga, causando uma deflexão nesse ponto . Essa deformação pode ser encontrada no apêndice do livro.
O enunciado quer que a gente mostre que:
A figura abaixo mostra esses dois casos.
Em segundo lugar, o enunciado quer que a gente encontre o valor do fator dinâmico da viga do Prob 10.72. O fator dinâmico vale:
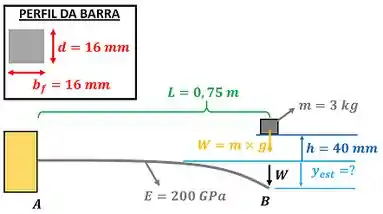
A figura abaixo mostra todos os dados do Prob. 10.72 que precisamos para achar o .
O do Prob 10.72 é encontrado a partir da equação presente no apêndice do livro.
A figura abaixo mostra os dados da questão 10.72.
No próximo passo vamos começar as contas determinando o valor de da letra (a).
Passo 2
da barra da letra (a) é obtido na equação presente no apêndice .
onde é o módulo de elasticidade do material da vida e é o momento de inércia do perfil da viga.
Pra achar , temos que lembrar que existe uma equação para calcular em função da força produzida pelo impacto do bloco de massa .
Substituindo essa equação na outra equação de , obtemos.
A equação resultante mostra que só falta achar uma equação de em função de para conseguir comparar com .
Achamos essa equação no apêndice do livro.
Ao invés de substituir na equação de , vamos descobrir quanto vale primeiro.
Passo 3
Se a gente reorganizar a equação de , conseguimos descobrir quanto vale .
Substituindo essa equação na fórmula de , achamos:
Agora, vamos substituir na equação de que deduzimos no passo 2.
Cortando nos dois lados achamos:
A equação acima, mostra que para achar , precisamos achar a raiz positiva do polinômio do segundo grau através da fórmula de Bhaskara. No entanto, para achar a raiz, precisamos achar os coeficientes do polinômio.
Pelo polinômio acima nós vemos que os coeficientes dele são:
Sabendo disso, somos capazes de calcular por Bhaskara.
Colocando o e o em evidência dentro da raiz:
Cortando o número 2 presente em todos os termos da fração e colocando em evidência:
Aeeeeee! Mostramos o que a letra (a) da questão queria!
Passo 4
Agora temos que resolver a letra (b) da questão, calculando o fator dinâmico do Prob. 10.72.
A única variável presente na equação do fator dinâmico que não conhecemos é o da viga. Calculamos esse valor, supondo que uma força de intensidade igual ao peso do bloco crrega a viga. Essa força vale:
Além disso, achamos uma equação para a partir do apêndice .
é o módulo de elasticidade do material da viga que vale , é o comprimento da viga que vale e é o momento de inércia da viga que pode ser calculado pela equação de momento de inércia para perfis quadrangulares abaixo.
Substituindo tudo isso na equação de , achamos:
Substituindo esse valor na equação do fator dinâmico e lembrando que o do Prob 10.72 vale :
Acaboooou! Encontramos o que a letra (b) da questão pedia!