Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 132
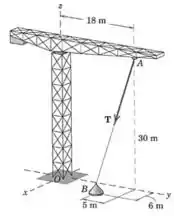
Ao levantar uma carga da posição , desenvolve-se no cabo uma força trativa de . Calcule o momento que produz em relação à base da grua de construção.
Passo 1
Vamos usar a definição de momento:
E então precisamos escrever cada um desses vetores:
Para escrever a força em forma vetorial vamos precisar de um vetor unitário na direção de :
E então a força é simplesmente o módulo multiplicado por :
Passo 2
Beleza, agora que já temos todos os vetores podemos calcular o produto vetorial:
E então:
Resposta
O momento que a força produz em relação à base é .
Exercícios de Livros Relacionados
Determine o módulo da reação do pino em A e o módulo e a direção da força de reação nos roletes. As polias em C e D são pequenas.
Determine as componentes x e y da força C , que o elemento B C exerce sobre o elemento A C D . Os cabos são enrolados firmemente em torno das duas polias, que estão aparafusadas entre si.
Se uma força F = 15N é necessária para soltar o pregador, quais são as reações normais em A e em B se F = 0 ?
A figura ilustra um problema comum associado a estruturas simples. Sob os carregamentos L , os caixilhos podem girar, a viga da cumeeira em A pode abaixar e as paredes B C e D E podem girar para fora,
A borboleta B da serra dobrável é apertada até que a tração na barra A B valha 200 N. Determine a força na lâmina de serra E F e o módulo F da força suportada pelo pino C .