Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 158
Determine as coordenadas do ponto no plano pelo qual passa a linha de ação da resultante do sistema de forças, para o sistema de forças do Prob. 2/149.
Passo 1
Temos no Prob. 2/149 uma força resultante N, gerando um momento em relação à origem de .
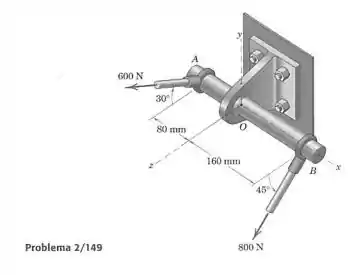
Como não é perpendicular a , haverá uma componente de igual a que será paralela à força. Então:
Sendo o vetor que devemos encontrar.
Passo 2
Temos então:
Passo 3
Como o vetor tem a mesma direção de , podemos escrever como:
Sendo o vetor o vetor unitário que indica a direção de . Podemos calculá-lo:
Então:
Passo 4
Agora resolvemos a equação:
Resposta
Exercícios de Livros Relacionados
13. Determine a intensidade do momento da força F → = 300 i - 200 j + 150 kN em relação ao eixo x. Expresse o resultado como vetor cartesiano.
14. Determine a intensidade do momento da força F → = 300 i - 200 j + 150 kN em relação ao eixo AO. Expresse o resultado como vetor cartesiano.
18. Determine o momento da força F em relação aos eixos x, y e z. Use uma análise escalar.
Determine o momento de binário resultante dos dois binários que agem sobre o encanamento. A distância de A a B é d = 400m m . Expresse o resultado como um vetor cartesiano.
Determine a distância d entre A e B tal que o momento de binário resultante tenha uma intensidade de M R = 20N ⋅ m .