Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 225

Uma nave espacial com uma massa de 260   k g está se deslocando com uma velocidade u = 30   000   k m / h na direção fixa x afastada de qualquer corpo celeste que a possa atrair. A nave espacial é estabilizada por rotação e gira em torno do eixo z na taxa constante θ ˙ = π 10   r a d / s . Durante um quarto de uma rotação de θ = 0 até θ = π 2 é ativado um jato que produz um empuxo T = 600   N de módulo constante. Determine a componente y da velocidade da nave espacial quando θ = π / 2 . Despreze a pequena variação na massa devida à perda de gases de escape através do bocal de controle e trate a nave espacial como uma partícula.

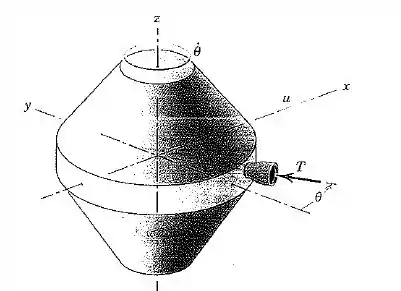
Passo 1

Bom galera, nesse exercício queremos determinar a componente y da velocidade quando θ = π 2 . Sabemos que

T y = 600 cos ⁡ θ

E

θ ˙ = π 10

Passo 2

Dessa forma, podemos escrever

d t = 10 π d θ

Por definição, temos que

∫ ∑ F y d t = m Δ v y

Passo 3

Substituindo, ficamos com

∫ 0 π 2 600 cos ⁡ θ 10 π d θ = 260 v y - 0

Resolvendo a integral e isolando v y , temos

v y = 7,35   m / s

Resposta

v y = 7,35   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O módulo de aterrissagem lunar de 200k g está descendo na superfície da Lua com uma velocidade de 6m / s quando seu retromotor é acionado. Se o motor produz um empuxo T por 4s que varia com o tempo co
Os dois motores de manobra orbital do ônibus espacial desenvolvem 26k N de empuxo cada um. Se o ônibus espacial está viajando em órbita a uma velocidade de 28000k m / h , quanto tempo levaria para alc
A gôndola de inspeção para um cabo suspenso está sendo puxada para cima no cabo inclinado à velocidade de 4m / s . Se o cabo de controle em A de repente se rompe, calcule o tempo t após a ruptura ocor
Um menino de 45k g corre e salta sobre seu trenó de 10k g com uma velocidade horizontal de 4,6m / s . Se o trenó e o menino deslizam 25 metros sobre a neve nivelada antes de atingir o repouso, calcule
Uma bala de 60g é disparada horizontalmente com uma velocidade v 1 = 600m / s contra o bloco de 3k g de madeira macia inicialmente em repouso sobre a superfície horizontal. A bala emerge do bloco com