Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 01

O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser representados por um único vetor tendo uma intensado m v G e atuando no ponto P, chamado de centro de percussão, o qual se encontra a uma distância r P / G = k G 2 / r G / O do centro de massa G. Aqui, k G é o raio de giração do corpo, calculado em relação a um eixo perpendicular ao plano do movimento e passando por G.

Passo 1

Antes de começar o exercício, devemos lembrar que o momento de inércia I G é dado em função do raio de giração através da seguinte fórmula:

I G = m k G 2  

Para nos auxiliar na resolução do exercício, usaremos o seguinte esquema para representar o problema:

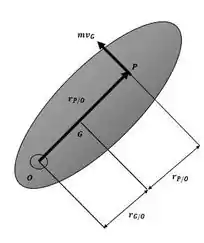
Passo 2

Dessa forma, conseguimos escrever o momento angular em relação ao ponto O da seguinte forma:

H O = r G / O + r P / G m v G = r G / O m v G + r P / G ( m v G )  

No entanto, sabemos que o último termo pode ser dado por:

r P / G m v G = I G ω

Dessa forma:

r G / O m v G + r P / G m v G = r G / O m v G + I G ω

Agora, substituindo a relação do passo 1:

r G / O m v G + r P / G m v G = r G / O m v G + ( m k G 2 ) ω

r P / G = k G 2 v G / ω

Passo 3

Por fim, sabemos ainda que a velocidade linear do centro de massa se relaciona com a angular pela seguinte fórmula:

v G = ω r G / O → r G / O = v G ω

Logo, substituindo isso na última equação do passo 2:

r P / G = k G 2 v G / ω → r P / G = k G 2 r G / O

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra esbelta uniforme tem uma massa de 30k g e é liberada a partir do repouso na posição próxima da vertical mostrada, onde a mola com rigidez de 150N / m está sem deformação. Calcule a velocidade
Cada um dos blocos quadrados maciços pode tombar girando no sentido horário a partir das posições de repouso mostradas. O suporte em O no caso (a) é uma rótula e no caso (b) é um pequeno rolete. Deter
O pequeno bloco de massa m desliza na ranhura radial lisa do disco, que gira livremente em seu mancal. Se o bloco é ligeiramente deslocado da posição central quando a velocidade angular do disco é ω 0
O anel de raio r com uma abertura está girando em torno de um eixo vertical através do seu centro O com uma velocidade angular constante ω . Utilize um elemento diferencial do anel e desenvolva expres
Que velocidade angular inicial no sentido horário ω a barra esbelta e uniforme de 75kg deve ter quando passa sobre a posição vertical θ = 0 para que consiga atingir a posição horizontal ( θ = 90 ° ) ?