Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 69
Localize o centro de gravidade (, ) da cantoneira de metal se o material for homogêneo e tiver uma espessura constante. Se a cantoneira estiver no plano horizontal mostrado, determine o ângulo máximo de inclinação que ela pode ter antes de cair, ou seja, começar a girar em torno do eixo .
Passo 1
O problema quer que a gente encontre um ângulo máximo antes de girar entorno do eixo , ou seja, o , é o ângulo em que o centro de massa da cantoneira está alinhada com a dobra dela. Da seguite forma:
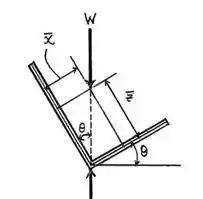
Então vamos calcular o centro de massa nos eixos e .
Passo 2
Então vamos dividir a cantoneira em alguns segmentos para facilitar no calculo:
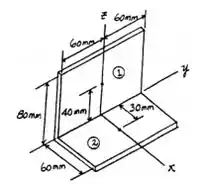
Agora, vamos fazer uma tabela para pegar as informações para calcular o centro de massa:
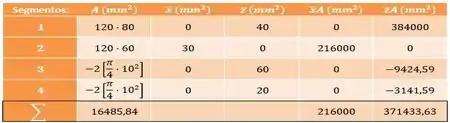
Passo 3
Então vamos calcular os centros de massa nos eixos e :
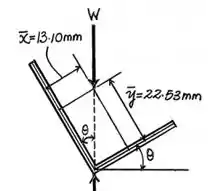
Então a gente calcula o ângulo com o inverso da tangente: