Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 67

Blocos uniformes com um comprimento L , e massa m são empilhados uns sobre os outros, com cada bloco ultrapassando o outro por uma distância d , conforme mostrado. Se os blocos estiverem colados, de modo que não possam tombar, determine a localização x - do centro de massa de uma pilha de n blocos.

Passo 1

O problema pede que encontremos o centro de massa da estrutura formada pelos blocos. Para começar, saiba o centro de massa resultante é dada por:

x - = x 1 - ⋅ m 1 + x 2 - ⋅ m 2 + x 3 - ⋅ m 3 … m T

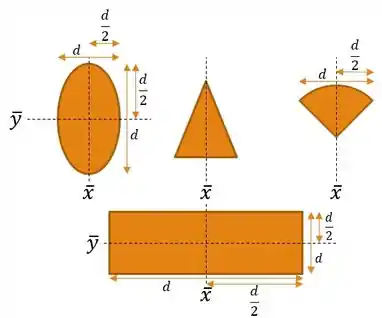
E pra facilitar, vou dar um dica importante: Quando o corpo é simétrico em um eixo e o corpo tem sua massa distribuída uniformemente, o centro de massa será no centro do corpo em relação ao eixo, a imagem agora vai facitilar muito sua vida:

Passo 2

Agora vamos calcular os centros de massa de cada bloco, vamos considerar os bloco de baixo pra cima 1 , 2 e 3 … respectativamente, então, vamos para calculo:

x - 1 = L 2

x - 2 = L 2 + d

x - 3 = L 2 + 2 d

Então notamos que:

x - n = L 2 + ( n - 1 ) d

Passo 3

Por último vamos calcular o centro de massa de todos os blocos juntos, é de certa forma uma média ponderada pela massa, assim:

x - = x 1 - ⋅ m 1 + x 2 - ⋅ m 2 + … + x n - ⋅ m n m T

x - = L 2 + ( n - 1 ) d ⋅ m + L 2 + ( n - 1 ) d ⋅ m + … + L 2 + ( n - 1 ) d ⋅ m n ⋅ m

x - = n L 2 m + n ( n - 1 ) d ⋅ m n m

Assim encontramos:

x - = L 2 + ( n - 1 ) d

Resposta

x - = L 2 + ( n - 1 ) d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Divida a placa em partes e, usando a grade para medição, determine aproximadamente a localização ( x - , y - ) do centróide da placa.
Para determinar a localização do centro de gravidade do automóvel, ele primeiro é colocado em uma posição nivelada, com as duas rodas em um lado apoiando sobre a plataforma P de uma balança. Nessa pos
Localize o centroide ( x - ,y - ) da área composta.
O carro se apoia em quatro balanças e, nessa posição, as leituras das rodas dianteiras e traseiras são idicadas por F A e F B . Quando as rodas traseiras são elevadas a uma altura de 0,9m acima das ba
Calcule o momento de primeira ordem de cada componente de superfície em relação a x e explique os resultados: