Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 73
Localize o centro de massa do conjunto. O hemisfério e o cone são compostos de materiais tendo densidades de e , respectivamente.
Passo 1
O problema quer que a gente encontre o centro de massa no eixo , para isso a gente vai calcular separadamente o hemisfério e o cone, e no final vamos calcular o do conjunto dele, assim:
Passo 2
Primeiro gente vai pegar os valores tabelados do centro de massa de um cone e de um hemisfério, você pode achar eles na internet, mas também fica no final do livro, nele a gente encontra que o centro de massa do:
Confere lá no final do livro, mas se precisar de ajuda tem umas vídeo aulas bem legais aqui mesmo no Responde aí.
Agora, vamos calcular os na estrutura do problema:
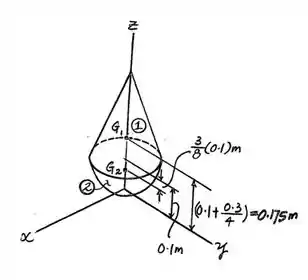
Passo 3
Agora, vamos calcular a massa dos dois corpos, mas agora vamos começar calculando o volume de cada corpo que dividimos, tem a formula do volume deles também no final do livro junto com o centro de massa que é:
Lembra que a questão passou umas densidades? Vamos usar ela agora para achar as massa, não precisa se preocupar com a unidade de massa porque ela não vai influenciar no resultado, mas pode converver se achar melhor para não se confundir, mas vamos lá:
Então, agora vamos para o centro de massa resultante: