Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 19

Localize o centroide bar x da área sombreada.

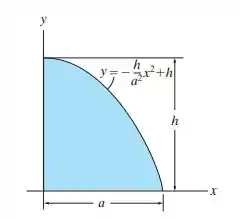
Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Para determinarmos o centroide bar y da área da área dada, precisamos utilizar a seguinte relação. Ela é dada por:

bar y = (int_A overset(tilde)(y) d A)/(int_A d A)

Onde A é a área abaixo do gráfico. Com isso, temos que o centroide está localizado em:

overset(tilde)(x) = x overset(tilde)(y) = (h + y)/(2)

Portanto, d A = y d x .

Passo 2

Em seguida, vamos resolver as integrais da relação para a posição do centroide separadamente. Primeiro, para o numerador, temos:

int_A overset(tilde)(x) d A = int_0^a (h^2 - ((h)/(a^2) x^2)^2) d x

Integrando:

= (384)/(7)

E para o denominador, temos:

int_A d A = int_0^a (h - (h)/(a^2) x^2) d x = h a + (h)/(3 a^2) a^3 = h ((4 a)/(3))

Com isso, a posição bar y do centroide vai ser:

bar y = (6 h)/(5)

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

bar y = (6 h)/(5)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo composto na figura é formado pela remoção de um semielipsoide de revolução de semieixo maior h e semieixo menor a / 2 a partir de um hemisfério de raio a . Determine (a) a coordenada y do cent
Para o suporte de batente mostrado na figura, determine a coordenadora z do centro de gravidade.
Para o suporte de batente mostrado na figura, determine a coordenadora x do centro de gravidade.
Determine o centroide das áreas planas a seguir.
Determine o centroide das áreas planas a seguir.