Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 94
O lustre é sustentado por três correntes que são concorrentes no ponto . Se a força resultante em possui uma intensidade de e é direcionada ao longo do eixo positivo, determine a força em cada corrente.
Passo 1
Fala galerinha bonita do RespondeAí, tudo belezinha?! Se liga só, o enunciado nos deu que 3 forças , e atuam através de uma corrente sustentando um lustre como no diagrama a seguir:
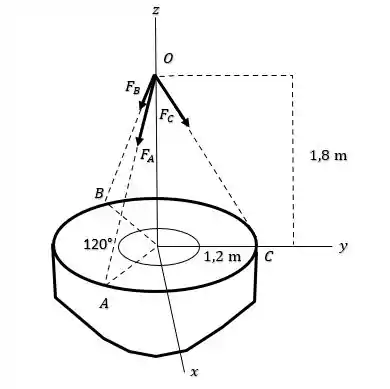
Sabendo que a resultante dessa força está no eixo e vale , ele pede pra gente descobrir a força que cada corrente exerce para manter o lustre sustentado. Belezoca, então bora lá!!
Passo 2
Pra gente começar, como a resultante está somente no eixo , teremos que:
Enquanto que no eixo :
MAAASS, malandragem aqui é que essa resultante vai ser consequência das componentes em das forças , e :
E como a intensidade da força em cada corrente é a mesma, vamos chamar de , teremos um diagrama como a seguir:
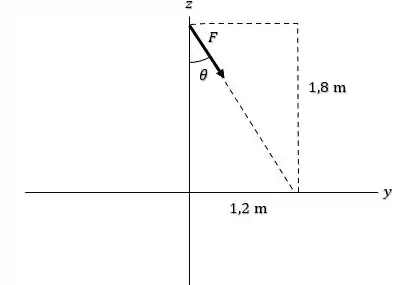
De modo que a componente no eixo de cada força vai ser dada como:
Logo, substituindo na resultante, teremos que:
Tal que:
Passo 3
E como temos um triângulo retângulo, o valor do cosseno de será:
Sendo assim, a força em cada corrente será expressa como:
Ou seja, cada corrente exerce uma força de de intensidade.
