Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 120

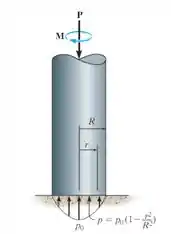
O mancal axial está sujeito a uma distribuição de pressão parabólica em sua superfície de contato. Se o coeficiente de atrito estático é μ s , determine o torque M necessário para superar o atrito e girar o eixo se ele suportar uma força axial P .

Passo 1

Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão! Para a base do mancal, temos:

Passo 2

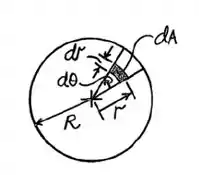
Essa questão não é tããão complicada, só precisamos ir com calma! Bom, o elemento diferencial de área pode ser escrito como d A = ( r d θ ) ( d r ) , levando a seguinte expressão para o diferencial da força P d P = p d A = p ( r d θ ) ( d r ) . Assim,

P = ∫ p d A = ∫ p o 1 - r 2 R 2 r d θ d r

P = p o ∫ 0 2 π d θ ∫ 0 R r 1 - r 2 R 2 d r

P = π R 2 p o 2 → p o = 2 P π R 2

Passo 3

O elemento diferencial da força normal que atua no mancal pode ser escrita como d N = p d A . Substituindo os valores dados na questão e encontrados no passo anterior, temos:

d N = p d A = p o 1 - r 2 R 2 r d θ d r

A expressão para p o nós encontramos no passo 2! Vamos subsitutir aqui:

d N = 2 P π R ² 1 - r 2 R 2 r d θ d r

Passo 4

O momento é o resultado de uma força atuando a uma determinada distãncia de um ponto de interesse, certo? No nosso caso, estmaos trabalhando com um diferencial de força de atrito a uma distância r do eixo do mancal axial. A equação para o momento fica da seguinte maneira:

M = ∫ r d F = ∫ μ s r d N

M = 2 μ s P π R 2 ∫ 0 2 π d θ ∫ 0 R r 2 1 - r 2 R 2 d r

O nos resulta em:

M = 8 15 μ s P R

Resposta

O torque M necessário para superar o atrito e girar o eixo é:

M = 8 15 μ s P R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

129- Determine a faixa de massas m do cilindro para a qual o sistema está em equilíbrio. O coeficiente de atrito entre o bloco de 50k g e o plano inclinado vale 0.15 e aquele entre a corda e o apoio c
145- A correia plana tem largura b = 50m m e está no limiar de deslizar conforme ela puxa a polia com raio r = 75m m através de um ângulo de contato de 180. Se a força trativa no lado frouxo da correi
136- A fita flexível presa em A faz uma meia volta em torno de cada um dos tambores de 100m m de diâmetro e termina na mola S , que é ajustada para produzir uma força trativa de 40N sobre a fita. Calc
135- Calcule o momento M aplicado ao cilindro inferior do par, ambos com 20k g , que permitirá que eles rolem para baixo lentamente. Os coeficientes de atrito estático e dinâmico para todas as superfí
144- O dispositivo está projetado para permitir um ajuste da força trativa horizontal T no cabo que passa em torno das duas polias fixas, para abaixar a massa m . Se o coeficiente de atrito entre o ca