Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 150
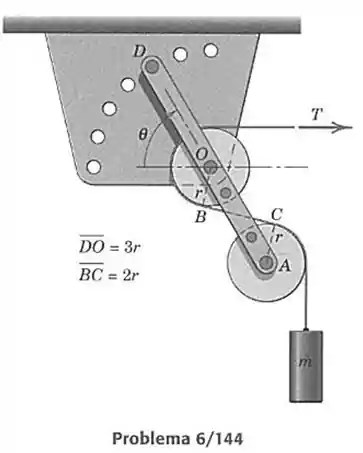
144- O dispositivo está projetado para permitir um ajuste da força trativa horizontal no cabo que passa em torno das duas polias fixas, para abaixar a massa . Se o coeficiente de atrito entre o cabo e as superfícies das polias vale , determine a razão , e faça um gráfico dessa razão em função de na faixa . Determine também o valor da força cisalhante no pino de ajuste em em termos de para .
Passo 1
A primeira abordagem para resolver essa questão é ser capaz de descobrir o ângulo de abraçamento do cabo nas polias e associar-las com . E para isso vamos adotar ângulos iguais a para a polia superior e para a inferior.
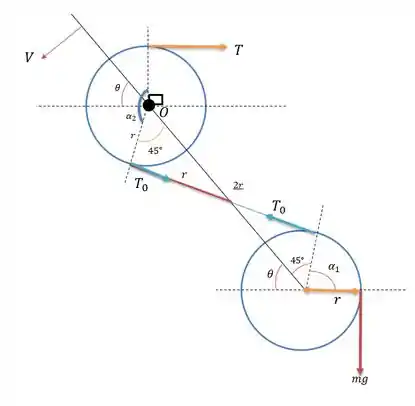
Para a polia superior temos o seguinte somatório de ângulos para dar um valor igual a
Agora para a polia inferior temos a seguinte somatória para dar um ângulo de meia volta:
Passo 2
Como a massa abaixa logo ela é maior que a força de tração logo:
E para manter esse abaixamento da massa temos que é maior que a força , logo:
Substituindo o valor de da segunda equação na primeira equação nós teremos a seguinte equação:
Como a multiplicação de potências de mesma base é igual a soma dos expoentes logo:
O gráfico para essa função pode ser vista abaixo:
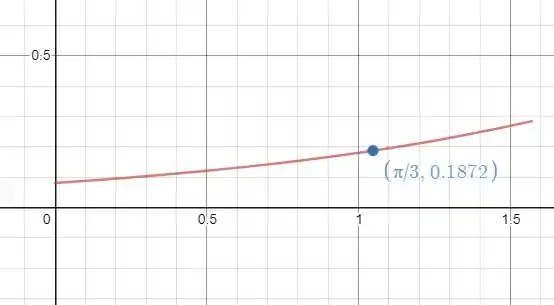
Eixo em radianos.
Passo 3
Para encontrar vamos fazer a somatória dos momentos em , para isso vamos desenhar o mesmo sistema porém com as medidas pertinentes para esse cálculo.
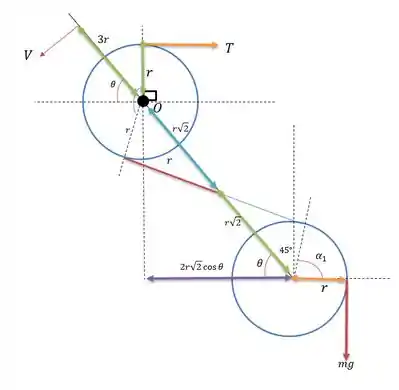
Logo a somatória dos momentos em das forças na figura será:
Para um valor de temos: