Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 139

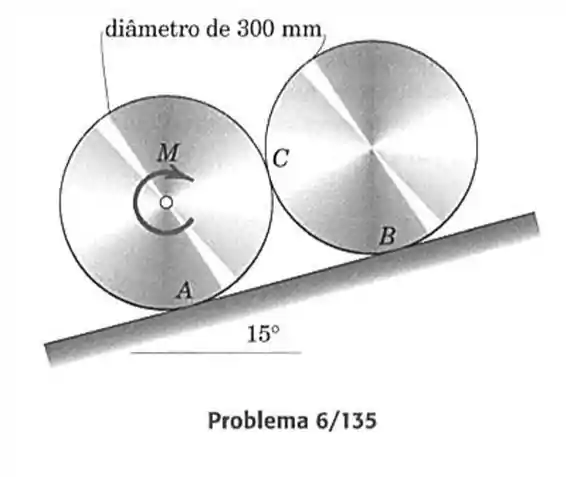
135- Calcule o momento aplicado ao cilindro inferior do par, ambos com , que permitirá que eles rolem para baixo lentamente. Os coeficientes de atrito estático e dinâmico para todas as superfícies de contato são e .

Passo 1

Mesmo tendo um momento indo para o sentido horário a roda desce, isso é o momento tende a parar o sistema, isso é fica no quase.

Vamos fazer o sistema de forças desse sistema, sabendo que existem forças de atrito entre os discos e entre o disco e o plano inclinado.

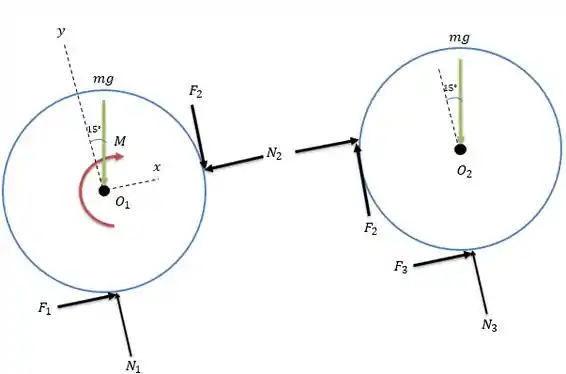
Porém não temos como dizer qual dessas forças de atrito tem coeficiente e então inicialmente vamos dizer que o piso tem coeficiente de atrito no chão vale e nos discos é .

Logo , e .

Passo 2

A somatória das forças verticais no disco vale:

E as horizontais no disco 1:

E a somatória dos momentos no disco vale (sentido horário positivo):

Passo 3

Agora fazendo a somatória das forças verticais no disco 2 nós teremos:

Agora as horizontais:

Agora a somatória dos momentos nos dá:

Passo 4

Muitas equações, muitas incógnitas, poucas certezas... vamos organizar as coisas um pouco:

Do primeiro disco temos:

Pro segundo disco:

Logo:

Onde:

Juntando com :

Da equação temos:

Da equação podemos escrever:

Substituindo os valores de massa e gravidade nós encontramos os seguintes valores para as normais:

Agora igualando temos:

Tanto faz se colocarmos valendo ou 0.6 o resultado de valerá um número menor a , então vamos assumir que vale e assumir que o sistema escorrega por ele.

Passo 5

Com essa suposição temos que:

Somente são válidas as últimas expressões encontradas para , e .

Como as forças e são menores que e respectivamente então a suposição está certa. Os discos não deslizam na superfície, o que faz com que o momento seja.