Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 136
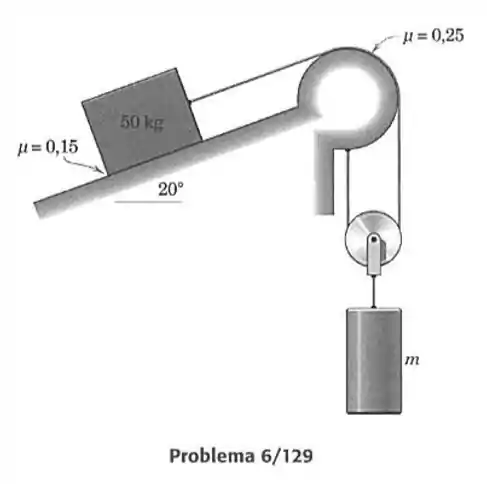
129- Determine a faixa de massas do cilindro para a qual o sistema está em equilíbrio. O coeficiente de atrito entre o bloco de e o plano inclinado vale e aquele entre a corda e o apoio cilíndrico vale .
Passo 1
Primeiramente vamos supor que o corpo de massa está descendo.
Isso faz com que a força de atrito no bloco tenda para a esquerda uma vez que o bloco tende a subir. Fazendo com que o sistema de forças fique da seguinte maneira.
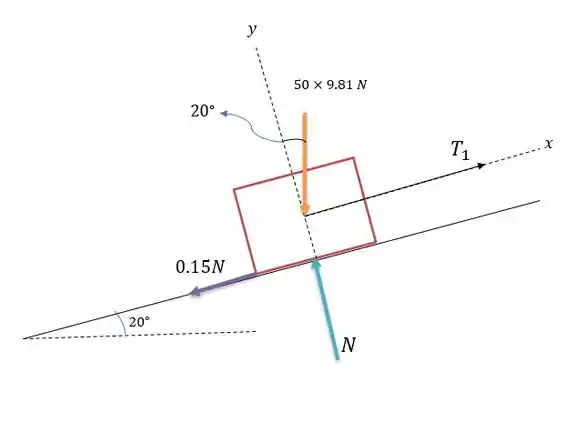
Fazendo a somatória das forças verticais no sistema nós teremos:
O que nos dá uma força de atrito igual a:
Com isso podemos calcular a força de tração na corda que será igual a:
Passo 2
Agora podemos analisar a polia para esse caso em que a massa está descendo.
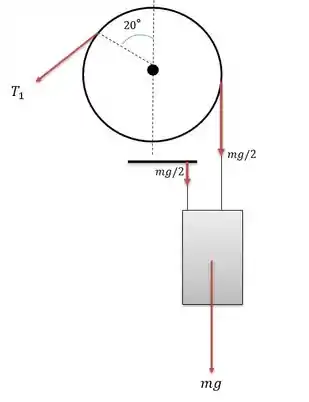
Onde nesse caso a tração será maior que . E o ângulo de abraçamento da polia com a correia será de:
Se convertida para radianos teremos:
Logo:
Passo 3
Agora vamos para o caso que o bloco está tendendo a subir, isso muda nosso sistema de forças no plano de modo que ele fica da seguinte maneira:
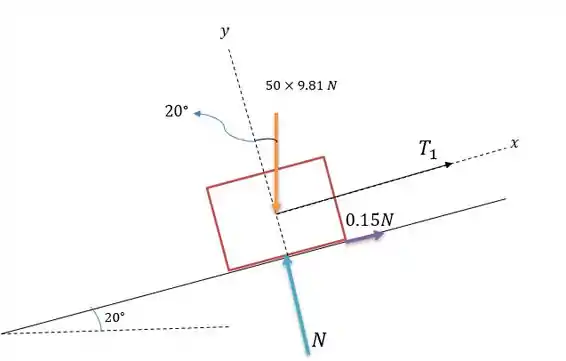
De modo que agora o bloco no plano tende a descer, fazendo com que a força de atrito agora tenha sentido para a direita.
A força normal continua sendo e a força de atrito também .
Fazendo a somatória das forças horizontais nesse sistema nós teremos:
Isso nos dá uma tração na corda igual a:
Passo 4
Agora vamos analisar o sistema de forças para a polia nesse caso:
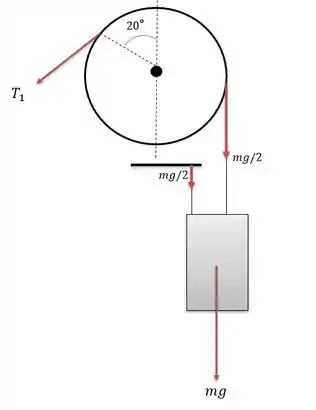
Como a massa está subindo nesse caso então será maior que .
Isolando temos:
Substituindo os valores encontramos:
Logo o intervalo de massas será: