A carga axial na coluna, que sustenta a viga de madeira mostrada, é de . Determine o comprimento da placa de apoio para que a tensão de esmagamento média na madeira seja de
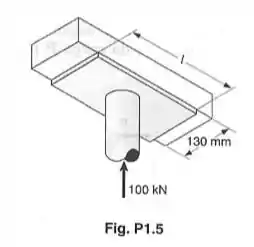
Passo 1
Neste exercício é pedida a tensão de esmagamento que é dada por:
Normalmente essa tensão de esmagamento é utilizada para pinos e aí fica da forma:
Mas aqui a questão foi boazinha e pede de toda a placa de apoio, que é de fato quem esmaga a coluna superior, então a área será a da própria placa (não vamos considerar a espessura aqui mas sim as dimensões e ).
Passo 2
Então a gente tem a área:
E a força
Passo 3
Agora basta substituir na equação
Aqui não precisamos nos preocupar com as grandezas porque a tensão está em a área em e a força em então ta tudo ok!