Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 183

A manivela AO gira no sentido horário com uma velocidade angular constante de 10 rad/s dentro de um arco limitado de seu movimento. Para a posição θ = 30 ° determine a velocidade angular da barra ranhurada CB e a aceleração de A quando medida em relação à ranhura em CB.

Passo 1

Bom pessoal, novamente nós temos mecanismos com deslizamento em ranhuras. Então nós vamos observar dois pontos coincidentes: o ponto A da barra AO e o ponto P da barra CB. Veja no esboço do mecanismo, usando o eixo x-y na barra CB.

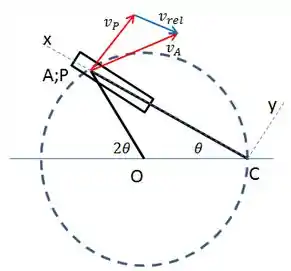
Beleza. Agora vamos calcular a velocidade do ponto A de acordo com a barra AO:

v A = ω O × r A O = - 10 k ^ × 0,2 ( c o s 30   i ^ + s e n 30   j ^ )

v A = 1,7 3 2 i ^ - 1 j ^   m / s

v A = 2   m / s

Pela relação dos vetores velocidade, podemos calcular v P e   v r e l :

v P = v A c o s 30 ° = 1,732   m / s

v r e l = v A s e n 30 ° = 1   m / s

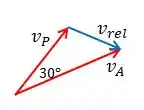
Podemos então calcular a velocidade angular de C por:

ω C = v P r P C = 1,732 0,2 3 = 5   r a d / s

Passo 2

Agora, vamos para o cálculo das acelerações.

O ponto A em relação à barra AO possui velocidade constante, tendo portanto apenas aceleração normal.

a A = - r ω O 2 = - 0,2 c o s 30   i ^ + s e n 30   j ^ - 10 2 = - 17,32 i ^ - 10 j ^   m / s 2

Vamos usar a equação da aceleração relativa entre os pontos A e C:

a A = a C + α × r A C + ω C × ω c × r A C + 2 ω C × v r e l + a r e l

Substituindo os valores, temos que:

- 17,32 i ^ - 10 j ^ = 0 + 0 - 0,2 3 i ^ 5 2 + 2 5 k ^ × - 1 i ^ + a r e l

Assim como v r e l , a a r e l também está na direção da ranhura. Portanto, decompondo a equação acima nas direções   i ^   e   j ^ :

- 17,32 i ^ = - 8,66 i ^ + a r e l

- 10 j ^ = 2 5 k ^ × - 1 i ^

Daí temos que:

a r e l = - 8,66   i ^   m / s 2

Resposta

a r e l = - 8,66   i ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O guindaste gira em torno do eixo z com uma taxa constante ω 1 = 0,6r a d / s , enquanto a lança gira para baixo com uma taxa constante ω 2 = 0,2r a d / s . Determine a velocidade e aceleração do pont
O guindaste gira em torno do eixo z com uma taxa de ω 1 = 0,6r a d / s , a qual está aumentando em ω ˙ 1 = 0,6r a d / s 2 . Além disso, a lança gira para baixo a ω 2 = 0,2r a d / s , a qual está aumen
O motor gira em torno do eixo z com uma velocidade angular constante ω 1 = 3r a d / s . Simultaneamente, o eixo O A gira com uma velocidade angular constante ω 2 = 6r a d / s . Além disso, o anel C de
No instante mostrado, o helicóptero está se deslocando para cima com uma velocidade v H = 1,2m / s e tem uma aceleração a H = 0,6m / s 2 . No mesmo instante, a fuselagem H , não o rotor horizontal, gi
No instante mostrado, o helicóptero está se deslocando para cima com uma velocidade v H = 1,2m / s e tem uma aceleração a H = 0,6m / s 2 . No mesmo instante, a fuselagem H , não o rotor horizontal, gi