Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 146

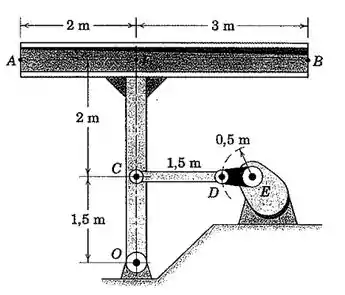
A manivela giratória ED e o elemento de ligação CD obrigam a estrutura rígida ABO a oscilar em torno de O. Para o instante representado, ED e CD são ambos perpendiculares a FO, e a manivela ED possui uma velocidade angular de 0,4 rad/s e uma aceleração angular de 0,06 rad/s², ambas no sentido anti-horário. Determine para esse instante a aceleração do ponto A, com respeito ao ponto B.

Passo 1

Pessoal, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do mecanismo.

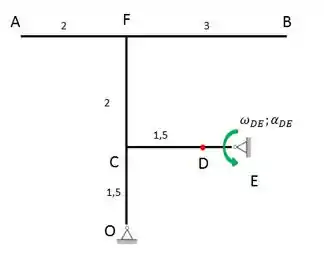
Podemos calcular a velocidade e aceleração do ponto D neste instante:

v D = ω D E × r D E = 0,4 × 0,5 = - 0,2   j ^   r a d / s

a D = - r D E ω D E 2 + α D E × r D E = - 0,4 2 - 0,5 i ^ + 0 , 06 k ^ × ( - 0,5 i ^ )

a D = 0,08 i ^ - 0 , 03 j ^   m / s 2

Ao observarmos a barra CD, vemos pelo ponto D calculado acima que não há velocidade na horizontal neste instante, e como o ponto C não pode se movimentar na vertical, sua velocidade resultante é nula. Em outras palavras, C é o Centro Instantâneo.

v C = 0

ω C D = v D r D C = - 0,2 1,5 = - 0,133   r a d / s

Ainda analisando a barra CD, vamos agora para a aceleração relativa entre C e D:

a C = a D + a C / D n + a C / D t

Onde:

a C / D n = - r C D ω C D 2 = - 0,13 3 2 - 1,5 i ^ = 0,027 i ^   m / s 2

a C / D t = α C D × r C D = - 1,5 α C D j ^ m / s 2

A aceleração de C pode ser calculada também pela análise da barra OC. É importante encontrar esta relação para poder substituir a C na equação da aceleração relativa C/D mostrada acima. Vamos lá então:

a C = a C n + a C t

a C n = - v C 2 r C O = 0                 ;                 a C t = α C O × r C O = - 1,5 α C O i ^

Agora sim, podemos substituir os valores encontrados na equação geral:

- 1,5 α C O i ^ = 0,08 i ^ - 0 , 03 j ^ + 0,027 i ^ - 1,5 α C D j ^    

Decompondo nas direções i ^   e   j ^ :

- 1,5 α C O i ^ = 0,08 i ^ + 0,027 i ^

0 = - 0 , 03 j ^ - 1,5 α C D j ^    

Resolvendo o sistema:

α C O = - 0,0713   k ^   r a d / s 2

α C D = - 0 , 0 3 k ^   r a d / s 2

Passo 2

Neste passo, vamos estabelecer a relação com a viga AB.

Como a estrutura ABO toda é rígida, as grandezas angulares calculadas valem para ela toda:

ω C O = ω A B = 0

α C O = α A B = - 0,0713   k ^   r a d / s 2

E finalmente, podemos calcular a aceleração relativa entre A e B:

a B / A = a B / A n + a B / A t

Onde:

a B / A n = - r A B ω A B 2 = 0   m / s 2

a B / A t = α A B × r B A = - 0,0713   k ^ × 5 i ^ = - 0,356 j ^   m / s 2

Portanto:

a B / A = - 0,356 j ^   m / s 2

Resposta

a B / A = - 0,356 j ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 0 , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.
Sabendo que a manivela AB gira em torno do Ponto A com uma velocidade angular constante de 900 rpm no sentido horário, determine a aceleração do pistão P quando θ = 60 ∘ .
Sabendo que a manivela AB gira em torno do Ponto A com uma velocidade angular constante de 900 rpm no sentido horário, determine a aceleração do pistão P quando 0 = 120 °.
A haste AB se move sobre uma pequena roda em C enquanto a extremidade A se move para a direita com velocidade constante vA. Usando o método da Seção 15.9, deduza expressões para a velocidade angular e
A manga BC é soldada a um braço que gira em torno de A com velocidade angular constante w. na posição mostrada a haste .DF está sendo movida para a esquerda a uma velocidade constante = 16 pol./s em r