Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 145

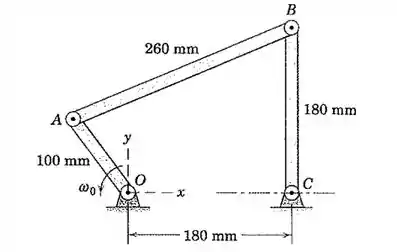
O mecanismo do Prob. 5/88 é apresentado novamente aqui. Se AO possui uma velocidade angular constante no sentido anti-horário ω O = 10   r a d / s , calcule a aceleração angular da barra AB para a posição onde as coordenadas de A são x = - 60 m m   e   y = 80 m m . A barra BC está vertical para essa posição. Resolva pela álgebra vetorial. (Utiliza os resultados do prob 5/88 para as velocidades angulares de AB e BC, que são ω B C = 5,83 k ^ r a d s   e   ω A B = 2,5 k ^ r a d / s . ) .

Passo 1

Pessoal, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do mecanismo.

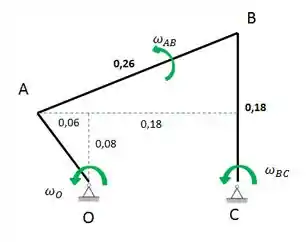
A partir daí, podemos começar a calcular algumas acelerações.

Vamos começar pela aceleração do ponto A pela barra AO. O enunciado diz que ω O é constante, portanto, α A O = 0 :

a A = a O + a A / O n + a A / O t = 0 - r A O ω A O 2 + 0

a A = - 100 - 0,06 i ^ + 0,08 j ^

a A = 6 i ^ - 8 j ^   m / s 2

De forma análoga, vamos fazer para a barra BC:

a B = a C + a B / C n + a B / C t = 0 - r B C ω B C 2 + α B C × r B C

a B = - 5,83 2 0,18 j ^ - 0,18 α B C i ^

a B = - 6,12 j ^ - 0,18 α B C i ^   m / s 2

E pela barra AB:

a B / A n = - r A B ω A B 2 = - 9 0,4   i ^ + 0,3 j ^   m / s 2

a B / A t = α A B × r B A = α A B - 0,3 i ^ + 0,4 j ^   m / s 2

Passo 2

Agora, vamos relacionar as acelerações de A e B usando a equação de aceleração relativa:

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = - r A B ω A B 2 = - 2 , 5 2 0,24   i ^ + 0 , 1 j ^   m / s 2

a B / A t = α A B × r B A = α A B - 0,1 i ^ + 0 , 2 4 j ^   m / s 2

Substituindo as variáveis encontradas no passo anterior:

- 6,12 j ^ - 0,18 α B C i ^ = 6 i ^ - 8 j ^ - 2,5 0,24   i ^ + 0,1 j ^ + α A B - 0,1 i ^ + 0,24 j ^  

Decompondo nas direções:

- 0,18 α B C i ^ = 6 i ^ - 6 , 2 5 0,24   i ^ + α A B - 0,1 i ^  

- 6,12 j ^ = - 8 j ^ - 6 , 2 5 + 0,1 j ^ + α A B + 0,24 j ^  

Resolvendo o sistema, encontramos as respostas:

α A B = 10,44   k ^   r a d / s 2

α B C = - 19,2   k ^   r a d / s 2

Resposta

α A B = 10,44   k ^   r a d / s 2

α B C = - 19,2   k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra A B de comprimento R = 300m m gira em torno A com velocidade angular constante ω 1 de 5r a d / s no sentido horário. Ao mesmo tempo, a barra B D de comprimento r = 160m m gira em torno de B co
O volante com raio de 18 pol. Está rigidamente preso a um volante de 1,5 pol. - eixo de raio que pode rolar ao longo de trilhos paralelos. Sabendo que no instante mostrado o centro do eixo tem uma vel
No sistema de engrenagens planetárias mostrado, o raio das engrenagens A, B, C e D é de 3 pol. E o raio da engrenagem externa E é de 9 pol. Sabendo que a engrenagem A tem uma velocidade angular consta
O disco mostrado tem uma velocidade angular constante de 500 rpm no sentido anti-horário. Sabendo que a haste BD tem 250 mm de comprimento, determine a aceleração do colar .D quando (a) θ = 90 ∘ , ( b
No compressor de ar de dois cilindros mostrado, as bielas BD e BE têm cada uma 190 mm de comprimento e a manivela AB gira em torno do Ponto fixo A com uma velocidade angular constante de 1500 rpm no s