Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 93

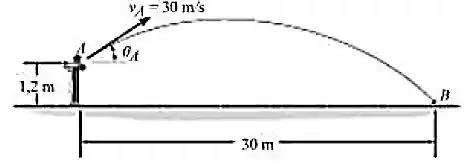
Uma máquina de lançar bolas de beisebol está ajustada de maneira que a bola de beisebol seja lançada com uma velocidade escalar de v A = 30 m/s. Se a bola atinge o solo em B, determine os dois ângulos possíveis θ A em que ela pode ter sido lançada.

Passo 1

Verifica-se que trata-se de um problema de lançamento oblíquo (lançamento de projétil). Nesse sentido adotar-se-á o sistema de coordenada x - y , por conveniência coincidindo com o ponto A , onde os eixos estão orientados positivamente para direita e para cima.

Pelas dimensões em x e y serem conhecidas, pode-se utilizar as seguintes equações: x = x 0 + v 0 t para o movimento horizontal e y = y 0 + v 0 y t + 1 2 a y t 2 para o movimento vertical.

Passo 2

Para o movimento horizontal do problema proposto,

x B = x A + v A x t

Sabendo que,

v a x = 30 cos ⁡ θ m / s

x a = 0

x b = 30   m

Substituindo os valores, pode-se reescrever como,

30 = 0 + 30 cos ⁡ θ t

t = 1 cos ⁡ θ                   ( 1 )

Passo 3

Para o movimento vertical do problema proposto,

y B = y A + v A y t + 1 2 a y t 2

Sabendo que,

v a y = 30 sen ⁡ θ   m / s

y a = 0

y b = - 1,2     m

a y = - g ∴   a y = - 9,81   m / s 2

Substituindo os valores, pode-se reescrever como,

- 1,2 = 0 + 30 sen ⁡ θ t + 1 2 ( - 9,81 ) t 2

4,905 t 2 - 30 sen ⁡ θ t - 1,2 = 0                           ( 2 )

Substituindo (1) em (2),

4,905 1 cos ⁡ θ 2 - 30 sen ⁡ θ 1 cos ⁡ θ - 1,2 = 0

Reorganizando

1,2 cos 2 ⁡ θ + 30 sen ⁡ θ cos ⁡ θ - 4,905 = 0                   ( 3 )

Resposta

Resolvendo a equação (3) para o ângulo θ , temos

θ 1 = 7,19 °  

θ 2 = 80,5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Observou-se que o tempo para a bola atingir o solo em B é 2,5s . Determine a velocidade v A e o ângulo θ A ao qual a bola foi jogada.
Um skatista deixa a rampa em A com uma velocidade inicial Va em ângulo 30°. Se ele atinge o solo em B, determine Va e o tempo de voo
Uma partícula move-se ao longo da trajetória circular de A para B em 1 s. Se ela leva 3 s para ir de A para C, determine a sua velocidade média quando ela vai de B para C.
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as