Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 55
Um marinheiro foi resgatado usando uma cadeira de contramestre suspensa por uma roldana que pode se movimentar livremente suportada pelo cabo ACB e é puxada com velocidade constante pelo cabo CD. Sabendo que e e que a cadeira de contramestre e o marinheiro juntos é 900 N, determine a tensão suportada pelo cabo ACB, pelo cabo de tração CD.
Passo 1
Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre com relação ao ponto C, temos:
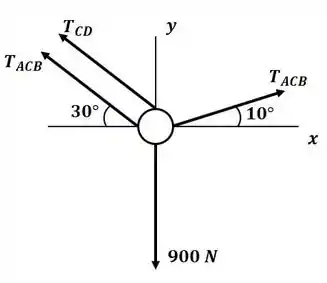
Passo 2
Agora que temos o DCL do problema, e temos 3 forças, mas 2 são desconhecidas, vamos decompor as forças nas direções e e aplicar o somatório de forças nessas duas direções. Começando pela direção :
Isolando temos a nossa equação 1:
Agora, aplicando o somatório na direção :
Simplificando a expressão, ficamos com:
Essa será nossa equação 2.
Passo 3
Agora, vamos substituir a equação 1 na equação 2:
Isolando e resolvendo, temos:
E agora, vamos subsituir esse valor na equação 1: