Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 94
94. Um diagrama esquelético de perna é mostrado na figura inferior. Aqui, podemos observar que a perna é suspensa pelo músculo quadríceps conectado ao quadril em e ao osso patela em . Este osso desliza livremente através da cartilagem na articulação do joelho. O quadríceps é mais extenso e conecta-se à tíbia em . Usando o sistema mecânico mostrado na figura superior para modelar a perna, determine a tração no quadríceps em e a intensidade da força resultante no fêmur (pino), , a fim de manter a anteperna na posição ilustrada. A perna possui uma massa de e um centro de massa em ; o pé possui uma massa de e um centro de massa em .
Passo 1
Para resolver esse problema podemos considerar somente a parte do joelho para frente.
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso é um pino, segundo a tabela do capítulo , seção , esse tipo de conexão por pino exerce força nas três direções dos eixos, mas como esse problema é bidimensional, podemos apenas considerar duas forças.
Para achar a intensidade de tendo suas componentes, basta calcular a norma, obtendo assim a intensidade.
Para achar a força exercida pela perna e pelo pé, basta calcular a força peso deles, que é só multiplicar pela gravidade .
Abaixo temos um diagrama de forças que representa nossa situação.
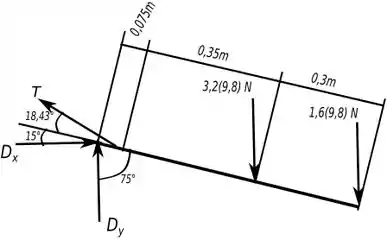
Os ângulos mostrados no diagrama podem ser achados pela relação:
E
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.
O macete é sempre começar com as equações que te oferecem menos incógnitas.
Passo 2
Primeiro vamos usar a equação de equilíbrio de equilíbrio referente ao momento em relação a , para acharmos .
Passo 3
Agora vamos usar as equações de equilíbrio referente a força em relação aos eixos e .
Passo 4
Agora vamos achar a intensidade de .