Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 79
O mastro está submetido às três forças mostradas. Determine os ângulos de direção coordenados , , de , de modo que a força resultante que atua no mastro seja zero.
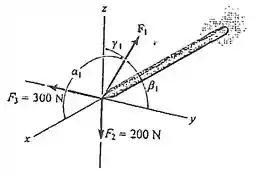
Passo 1
Aqui como nossas forças estão nos eixos não precisamos de muita conta, para a resultante ser zero, nossa precisa ter o módulo igual das componentes das outras forças com o sentido oposto, ficaremos com:
E a intensidade do seu módulo será:
Passo 2
Só falta encontrar os ângulos de direção coordenados de , sendo:
Então:
Resposta
Exercícios de Livros Relacionados
Uma força F → de intensidade 210 N atua na origem de um sistema de coordenadas. Sabendo que F x = 80N , θ z = 151,2 ° e F y0 , determine, ( a ) os componentes F y e F z , ( b ) os ângulos θ x e θ y .
Uma placa circular horizontal está suspensa, como mostra a figura, por três fios que estão ligados a um suporte D e formam ângulos de 30° com a vertical. Sabendo que a componente z da força exercida p
Uma placa circular horizontal está suspensa, como mostra a figura, por três fios que estão ligados a um suporte D e formam ângulos de 30° com a vertical. Sabendo que a componente x da força exercida p
42- Sabendo que a tensão no cabo A D é de 40 5N , determine a ) o ângulo entre o cabo A D e a barra A B , b ) a projeção em A B da força exercida pelo cabo A D no ponto A .
2.92 Encontre a intensidade, a direção e o sentido da resultante das duas forças mostradas, sabendo que P=400N e Q=300N.