Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 66
O mastro uniforme de possui uma massa de e é articulado em sua extremidade inferior a um suporte fixo junto a . Se o guincho desenvolve um torque de partido de , calcule a força total suportada pelo pino em quando o matro começa a ser erguido de seu apoio em . Encontre também a aceleração angular correspondente do mastro. O cabo em está horizontal e as massas das polias e do cabo são desprezíveis.
Passo 1
Primeiro vamos calcular a força realizada no ponto quando aplicamos um torque no guincho.
Já que o raio do guincho é:
A força associada ao momento seria dada pela seguinte fórmula:
Mas como o cabo está conectado ao ponto por uma polia móvel, temos que colocar um fator de nessa equação:
Passo 2
Agora queremos encontrar a aceleração angular do mastro:
O momento de inércia em relação ao ponto é:
E as únicas forças que produzem momento sobre esse corpo são as componentes perpendiculares do peso e da tração (que favorecem a rotação em direções contrárias):
E então:
Passo 3
Agora podemos usar a segunda lei de Newton nas direções tangencial e normal para encontrar a força em .
Começando pela direção tangencial:
A aceleração tangencial do centro de massa é , então:
E agora vamos encontrar as forças que agem nessa direção:
E então:
Passo 4
Agora vamos analisar a direção normal:
As forças que agem nessa direção são as seguintes:
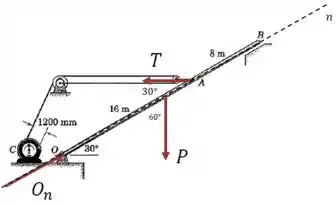
E então podemos calcular o módulo da força total exercida em :
Resposta
A aceleração angular é e a força total suportada pelo pino é .