Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 104
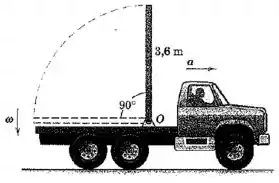
O mastro uniforme de é articulado à plataforma do caminhão e liberado a partir da posição vertical quando o caminhão parte do repouso com uma aceleração de . Se a aceleração permanece constante durante o movimento do mastro, calcule a velocidade angular do mastro quando atingir a posição horizontal.
Passo 1
Geralmente, quando queremos encontrar a velocidade angular para um determinando deslocamento angular (nesse caso, ), temos que usar a seguinte relação:
E quando integramos dos dois lados:
O nosso problema passa a ser o seguinte: encontrar uma expressão que dê a aceleração angular em função de .
Passo 2
Como queremos encontrar uma aceleração angular em torno de , vamos montar uma equação de momentos em relação ao ponto :
A única força que produz momento em relação ao ponto é uma componente da força peso, agindo no centro de massa do mastro:
E o momento de inércia do mastro em relação a um eixo que passa pelo ponto é:
Agora vamos olhar para o último termo, que considera os momentos da força resultante que age no centro de massa.
Bom, o centro de massa está em rotação em torno do ponto , certo? Então ele terá uma aceleração tangencial e uma centrípeta associadas a essa rotação.
Além disso, tem um aceleração de translação do centro de massa, associado ao movimento do caminhão para frente:
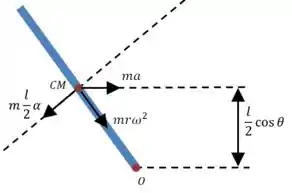
E então:
Agora vamos substituir os valores para encontrar uma função . Primeiro dividimos toda a equação por :
Passo 3
Agora vamos subsituir essa função na equação que escrevemos no primeiro passo:
Vamos resolver cada termo da integral separadamente:
Então:
Resposta
A velocidade angular do mastro quando atinge a posição horizontal é .