Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 16

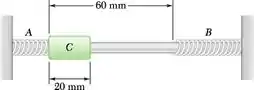
Um colar C de 8 kg pode deslizar sem atrito sobre uma barra horizontal entre duas molas idênticas A e B nas quais não está preso. Cada mola tem uma constante k = 600 N/m. O colar é empurrado para a esquerda contra a mola A, comprimindo esta em 20 mm, e liberado na posição mostrada na figura. Ele então desliza ao longo da barra para a direita e atinge a mola B. Após comprimir esta mola em 20 mm, o colar desliza para esquerda e atinge a mola A, que é comprimida de 20 mm. O ciclo é então repetido. Determine (a) o período do movimento do colar, (b) a velocidade do colar 1,5 s depois de ter sido liberado. (Nota: Isto é um movimento periódico, mas não um movimento harmônico simples.)

Passo 1

O enunciado pede que a gente determine (a) o período do movimento do colar, (b) a velocidade do colar 1,5 s depois de ter sido liberado. (Nota: Isto é um movimento periódico, mas não um movimento harmônico simples.)

  1. Para qualquer mola,

    2. τ n = 2 π k m C

    τ n = 2 π 600   N/m 8   kg

    τ n = 0.7255   s

    Passo 2

    O ciclo completo é 1234, 4321.

    O tempo de 1 a 2 é ( τ n / 4 ), que é o mesmo que o tempo de 3 a 4, 4 a 3 e 2 a 1.

    Assim, o tempo durante o qual as molas são comprimidas são 4 τ n / 4 = τ n = 0.7255   s .

    Passo 3

    Velocidade em 2 ou 3.

    Use a conservação de energia.

    v 1 = 0                 T 1 = 0                 V 1 = 1 2 k x 2 = 1 2 600   N/m 0.020   m 2

    V 1 = 0.120   J

    T 2 = 1 2 m v 2 2 = 1 2 8   kg v 2 2               T 2 = 4 v 2 2

    V 2 = 0

    T 1 + V 1 = T 2 + V 2                 0 + 0.120 = 4 v 2 2               v 2 = 0.1732   m/s

    Passo 4

    Tempo de 2 a 3 é

    t 2 - 3 = 0.020   m 0.1732   m/s = 0.11545   s

    e é igual ao tempo de 3 a 2.

    Assim, o tempo total para um ciclo completo é

    τ c = τ n + 2 t 2 - 3 = 0.7255 + 2 0.11545 = 0.9564

    Passo 5

  2. De (a), em 0,9564, a mola A está novamente totalmente comprimida. A mola B é comprimida pela segunda vez em 1,5 ciclos ou (1,5) (0,9564) = 1,4346 s. Em 1,5 s, o colar ainda está em contato com a mola B se movendo para a esquerda e está a uma distância Δ x da deflexão máxima de B igual a

Δ x = 20 - 20 cos ⁡ 2 π 0.7255 1.5 - 1.4346

Δ x = 20 - 16.877 = 3.123   mm

Assim, o colar C é 60 - 3.123 = 56.877   mm de sua posição inicial.

Resposta

a )   τ c = 0.956   s

b )   56.9   mm da posição inicial

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo robótico do Prob. 6/60 é reapresentado aqui. O elemento A B está girando em torno da articulação A com uma velocidade angular no sentido anti-horário de 2r a d / s , e essa velocidade es
O ioiô possui uma massa m e um raio de giração k em relação ao seu centro O . O cordão tem um comprimento máximo y = L e se enrola em torno do pequeno núclo central de raio r com sua extremidade fixad
Uma placa plana uniforme de massa m na forma de um quadrante circular de raio r está fixada ao aro de massa desprezível na posição indicada. Se o aro e o quadrante são liberados a partir do repouso ne
A figura mostra a vista lateral de uma laje de concreto uniforme com uma massa de 12t . A laje está sendo içada lentamente pelo guincho D por meio do cabo preso ao carrinho. Na posição θ = 60 ° , a di
Em uma investigação do “efeito de chicote” resultante de colisões trasieras, a rotação brusca da cabeça é modelada utilizando uma esfera maciça homogênea de massa m e raio r que gira em torno de um ei